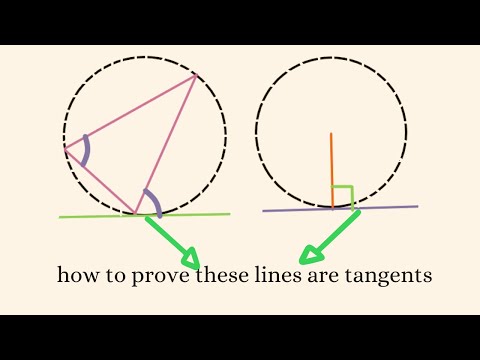
Prove that tangent at the ends of any chord of a parabola

Prove that tangent at the ends of any chord of a parabola #mathematics #calculus #geometry
Let's consider a parabola with its axis parallel to the y-axis and its vertex at the origin (0,0). Without loss of generality, let the equation of the parabola be \(y = ax^2\), where \(a\) is a non-zero constant.

Now, let \(AB\) be any chord of the parabola with \(A\) and \(B\) as the points on the parabola. Without loss of generality, let \(A\) and \(B\) be symmetric with respect to the y-axis, so \(A\) is \((-p, ap^2)\), \(B\) is \((p, ap^2)\), and \(O\) is the midpoint of \(AB\), which is the origin \((0,0)\).

The equation of the chord \(AB\) is \(y = ax^2 - ap^2\).

Now, let \(P\) and \(Q\) be the points where the tangents at the ends of the chord \(AB\) meet the x-axis. Without loss of generality, let \(P\) be the point where the tangent at \(A\) meets the x-axis, and \(Q\) be the point where the tangent at \(B\) meets the x-axis.

The equation of the tangent at \(A\) is given by \(y - ap^2 = 2ap(x + p)\), and the equation of the tangent at \(B\) is given by \(y - ap^2 = 2ap(x - p)\).

Setting \(y = 0\) in both equations to find the points of intersection with the x-axis, we get:
1. For tangent at \(A\): \(0 - ap^2 = 2ap(x + p)\)
2. For tangent at \(B\): \(0 - ap^2 = 2ap(x - p)\)

Solving these equations gives the x-coordinates of \(P\) and \(Q\):
1. For tangent at \(A\): \(x_P = -2p\)
2. For tangent at \(B\): \(x_Q = 2p\)

Now, the midpoint \(O\) of the chord \(AB\) is the origin \((0,0)\), which is also the midpoint of \(P\) and \(Q\).

Since \(O\) is the midpoint of \(PQ\), \(OP = OQ\), and the line joining \(P\) and \(Q\) passes through the origin \((0,0)\). This line is the diameter of the parabola that bisects the chord \(AB\).

Therefore, we have shown that the tangents at the ends of any chord of a parabola meet on the diameter that bisects the chord.
Hashtags::
#Parabola #Geometry #Tangent #Chord #Diameter #Mathematics #ConicSections
Keywords:
1. Parabola
2. Chord
3. Tangent
4. Diameter
5. Bisect
6. Intersection
7. Symmetry
8. Midpoint
9. Origin
10. Conic Section
11. Tangent Equation
12. Chord Equation
13. Tangent Intersection
14. Proof
15. Geometry
16. Coordinate Geometry
17. Vertex
18. Focus
19. Axis of Symmetry
20. Mathematical Proof