filmov
tv
Find all Zeros of a Polynomial Function given a Factor or Zero

Показать описание
We will use synthetic division to divide out a given zero or factor from a polynomial function. Then factor the quotient which is quadratic. As a bonus, I will sketch a rough graph of the polynomial function and write it in factored form! All good test questions to be prepared for!
Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem
How To Find the Zeros of The Function
Finding All of the Zeros of a Polynomial Including Complex
Find the Zeros of a Polynomial and Their Multiplicities
Ex 2: Find the Zeros of a Polynomial Function - Real Rational Zeros
How to Find Real Zeros of Any Polynomial Function
❖ Finding all the Zeros of a Polynomial - – Step-by-Step Example Using Rational Roots Test ❖
Given a Polynomial Function Find All of the Zeros
Taking it to the max: optimization problems
How to Use Factoring to Find All of the Zeros of a Polynomial Function
Find All of the Zeros of a Polynomial
How to Find the zeros of a function
Find all zeros of a polynomial function
List all possible and find all zeros of a polynimial function
Find all of the Zeros of a Polynomial by Factoring
Using the rational zeros theorem to find all the zeros of a function
Given an Complex Zero, Find All the Zeros With Quadratic Formula
Rational Zero Theorem | Find all zeros of a polynomial function (quadratic formula)
Given the Factors Determine All Zeros and Write as a Product of its Factors
Find All the Zeros of a Polynomial by Factoring
for x^3 - 2x^2 + 2x Find all zeros of P, real and complex.
for x^4 + 4x^2 Find all zeros of P, real and complex.
How to Determine All of the Zeros of a Polynomial
How to find the zeros of an quadratic equation - Free Math Help
Комментарии
 0:12:18
0:12:18
 0:05:48
0:05:48
 0:05:35
0:05:35
 0:04:30
0:04:30
 0:05:16
0:05:16
 0:06:52
0:06:52
 0:10:12
0:10:12
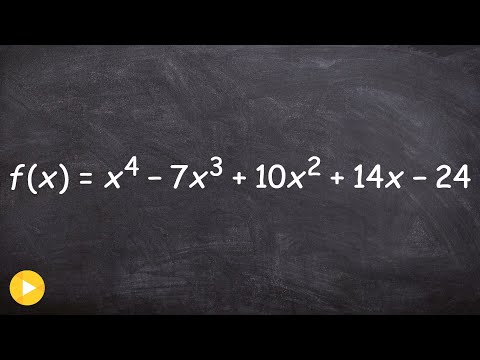 0:11:31
0:11:31
 1:01:41
1:01:41
 0:02:38
0:02:38
 0:06:20
0:06:20
 0:17:42
0:17:42
 0:04:07
0:04:07
 0:06:14
0:06:14
 0:01:51
0:01:51
 0:09:57
0:09:57
 0:07:13
0:07:13
 0:05:55
0:05:55
 0:05:35
0:05:35
 0:03:13
0:03:13
 0:01:26
0:01:26
 0:01:02
0:01:02
 0:09:37
0:09:37
 0:02:52
0:02:52