filmov
tv
Can We Find The Inverse of A Cubic Function?

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ f(x) = x^3 + 3x, find f^(-1)(x) = ?
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ f(x) = x^3 + 3x, find f^(-1)(x) = ?
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
How To Find The Inverse of a Function
Inverse Matrices and Their Properties
How To Find The Inverse of Exponential Functions
Finding the inverse of a function
Inverse Functions
How to write the inverse of a function when it is a fraction
Find The Inverse Function | Algebra 2
Step by Step process to find the inverse of a linear function
Most People Failed This | Finding The Inverse Of A Function | Can You Solve It? - SAT Math
Verifying Inverse Functions | Precalculus
How to find the inverse of a Matrix
Inverse of a 2x2 Matrix
How to find Inverse of a Matrix Using Calculator #youtubeshorts #shortsviral #viral
Inverse of a 3x3 Matrix
How to find the inverse of a function then determine domain and range
How to Find the Inverse of a 2x2 Matrix | Step-by-Step Explanation
Inverse of a 2x2 matrix | Matrices | Precalculus | Khan Academy
How to calculate inverse tan in scientific calculator #scintific #calculator #studenthacks
Find the Inverse of a Function Algebraically
How to find out Multiplicative Inverse of any Number ? // 👍
Find the Inverse of a Function
Evaluating Inverse Trigonometric Functions
How to find the inverse and then determine if the inverse is a function
How to Find the Inverse of a Function
Комментарии
 0:11:36
0:11:36
 0:12:00
0:12:00
 0:14:41
0:14:41
 0:03:27
0:03:27
 0:06:29
0:06:29
 0:03:25
0:03:25
 0:00:58
0:00:58
 0:02:37
0:02:37
 0:02:19
0:02:19
 0:12:06
0:12:06
 0:00:56
0:00:56
 0:10:11
0:10:11
 0:00:50
0:00:50
 0:15:21
0:15:21
 0:03:02
0:03:02
 0:04:35
0:04:35
 0:02:48
0:02:48
 0:00:15
0:00:15
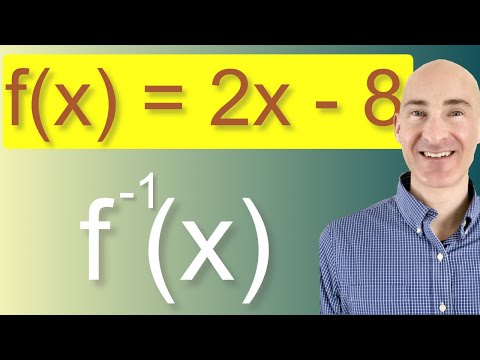 0:02:17
0:02:17
 0:00:23
0:00:23
 0:01:01
0:01:01
 0:22:47
0:22:47
 0:02:41
0:02:41
 0:06:17
0:06:17