filmov
tv
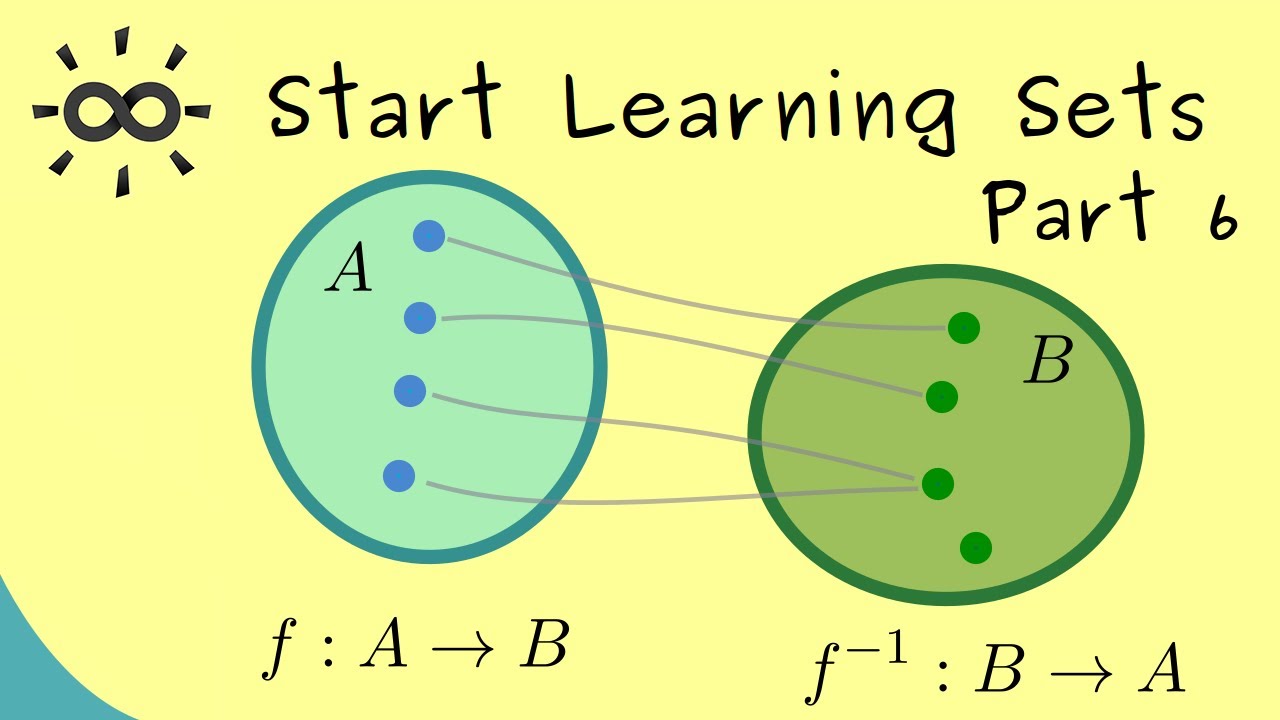
Start Learning Sets 6 | Injectivity, Surjectivity and Bijectivity
Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Start Learning Sets. We discuss basic definition, like union and intersection, and also go into the details of maps and functions. I hope that it will help everyone who wants to learn about it.
x
#StartLearningMathematics
#Mathematics
#LearnMath
#calculus
x
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Start Learning Sets 6 | Injectivity, Surjectivity and Bijectivity [dark version]
Start Learning Sets 1 | Overview and Element Relation [dark version]
RATING MY OLD NAIL SETS (back when i was learning)🧍🏻♀️ #youtubeshorts #pressons #shorts
Start Learning Sets 5 | Range, Image and Preimage
Start Learning Sets 2 | Predicates, Equality and Subsets
Pororo Crong Educational Learning Set Part 2 #asmr #pororo
Fun & Learning! 6-in-1 Baby Toy Set: Montessori, Bath, Sensory & More!
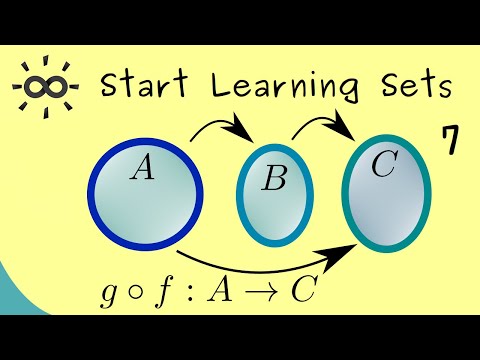
Start Learning Sets 7 | Composition of Maps
Unlock Your Ultimate Workout with Accessory Exercises!
Was this $90 LEGO Minifigure lot worth it? • Part 1 #lego #legominifigures #powerminers #legos
Set Theory | All-in-One Video
Pororo Crong Educational Learning Set #asmr #pororo
First Letters Magnets Early Learning Set For Kids Ages 5+ to Learn Spelling with 140+ Magnets
Математичний набір 'Сенсорні черепахи' Learning resources 95328 Tactile Turtles Maths Acti...
Limited Edition: Learn to Pray Box (Girl’s Set) #faithinspired #islamicgifts #muslimgifts
Baby Firsts EARLY LEARNING Box Set includes 6 Board Books and 6 Stacking Blocks
Baby Firsts EARLY LEARNING Box Set includes 6 Board Books and 6 Stacking Blocks
Collins Easy Learning Starter Set Ages 3–5 Ideal for home learning 6 Books Pack
Was this $90 LEGO Minifigure lot worth it? • Part 2 #lego #legominifigures #legocastle #legos
Let's Build Numberblocks Multi-Click Blocks 1-10 Play and Learn Set || Keiths Toy Box
Shapes All Around Learning Set #backtoschool #education
Baby Firsts Early Learning Box Set (6 Learning Board Books)
'Create & Learn: 3Doodler Start+ Essentials 3D Pen Set for Kids'#amazon #products #sho...
Action Learning Sets HD
Комментарии
 0:05:56
0:05:56
 0:06:27
0:06:27
 0:00:59
0:00:59
 0:09:54
0:09:54
 0:11:49
0:11:49
 0:00:37
0:00:37
 0:00:39
0:00:39
 0:05:58
0:05:58
 0:00:53
0:00:53
 0:01:01
0:01:01
 0:29:24
0:29:24
 0:00:29
0:00:29
 0:00:30
0:00:30
 0:00:29
0:00:29
 0:01:01
0:01:01
 0:01:14
0:01:14
 0:03:55
0:03:55
 0:00:35
0:00:35
 0:01:01
0:01:01
 0:08:36
0:08:36
 0:00:29
0:00:29
 0:00:52
0:00:52
 0:00:29
0:00:29
 0:03:09
0:03:09