filmov
tv
Given the equation of an parabola, find the vertex, focus and directrix
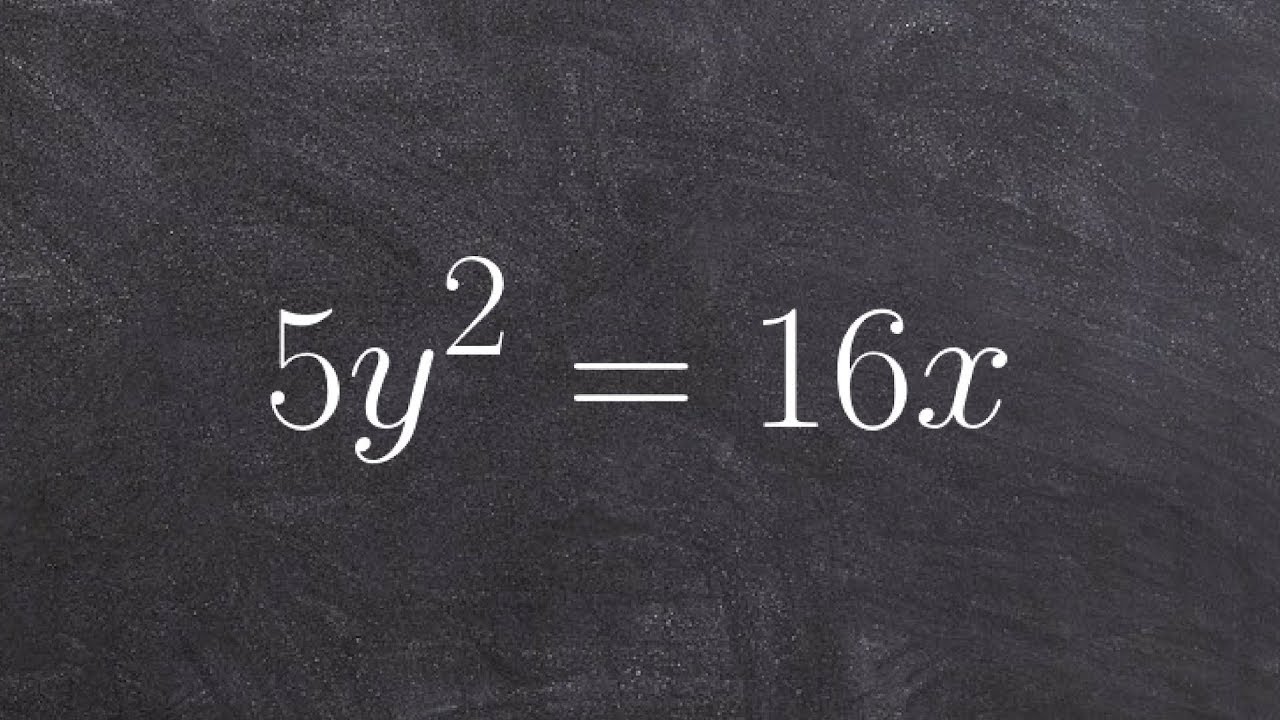
Показать описание
Learn how to graph a horizontal parabola. A parabola is the shape of the graph of a quadratic equation. A parabola is said to be horizontal if it opens to the left or opens to the right. A horizontal parabola results from a quadratic equation in which the y part of the equation is squared.
To sketch the graph of a parabola, we first identify the vertex, the focus and the directrix. To do this, we first write the equation in the form (y - k)^2 = 4p(x - h), where (h, k) is the vertex and p is the distance between the vertex and the focus.
After expressing the equation in the form (y - k)^2 = 4p(x - h), the vertex is given by (h, k), the focus is given by (h + p, k) and the directrix is given by the line x = h - p. After obtaining the vertex, the focus and the directrix, we can then sketch the parabola.
#conicsections #parabolaconicsections
To sketch the graph of a parabola, we first identify the vertex, the focus and the directrix. To do this, we first write the equation in the form (y - k)^2 = 4p(x - h), where (h, k) is the vertex and p is the distance between the vertex and the focus.
After expressing the equation in the form (y - k)^2 = 4p(x - h), the vertex is given by (h, k), the focus is given by (h + p, k) and the directrix is given by the line x = h - p. After obtaining the vertex, the focus and the directrix, we can then sketch the parabola.
#conicsections #parabolaconicsections
 0:08:32
0:08:32
 0:10:05
0:10:05
 0:07:38
0:07:38
 0:01:54
0:01:54
 0:05:07
0:05:07
 0:09:35
0:09:35
 0:08:28
0:08:28
 0:02:09
0:02:09
 0:00:52
0:00:52
 0:05:52
0:05:52
 0:04:37
0:04:37
 0:02:26
0:02:26
 0:05:30
0:05:30
 0:03:25
0:03:25
 0:06:07
0:06:07
 0:02:01
0:02:01
 0:06:49
0:06:49
 0:06:56
0:06:56
 0:04:50
0:04:50
 0:02:39
0:02:39
 0:04:41
0:04:41
 0:07:37
0:07:37
 0:04:00
0:04:00
 0:06:06
0:06:06