L60: Lagrange's Theorem and Fermat's Little Theorem

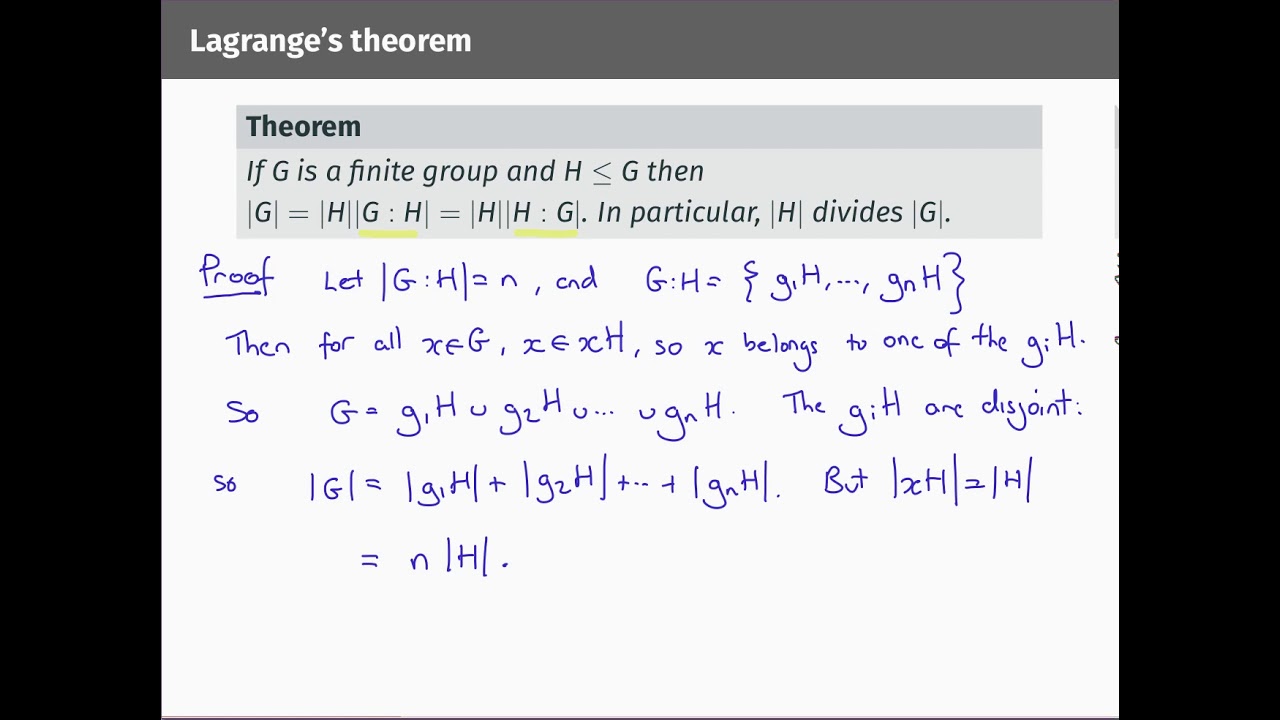
Proof of Lagrange's theorem: if H is a subgroup of a finite group G then |G| = |H| |G:H| = |H| |H:G|. Corollaries: the order of an element of a finite group divides the order of the group, and if you raise any element to the power |G| you get the identity. Proof of Fermat's Little Theorem (that if p is prime and a isn't divisible by p then a^{p-1} is congruent to 1 mod p) using Lagrange's Theorem. Finding large powers modulo primes.