Complex Number Addition on the Argand Plane

In this video, I demonstrate the similarities between complex number addition and vector addition, when visualised geometrically on the complex plane.

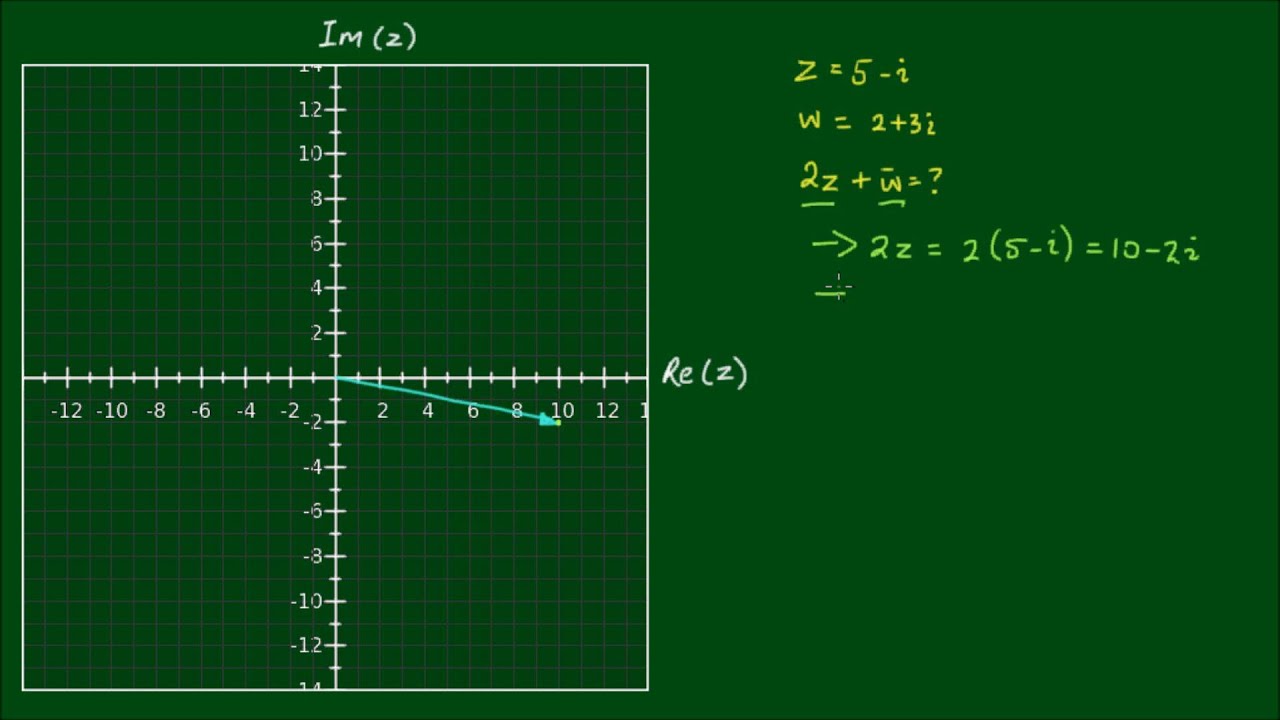
Here, we have two complex numbers:

z = 5 - i
w = 2 + 3i

We want to represent the addition of 2z plus the complex conjugate of w on the complex plan. That is...

2z + w_bar

The coordinates of 2z = 10 - 2i are (10, -2). We can represent this on the complex plane by drawing a vector from the origin (0,0) in this coordinate.

The coordinates of w_bar = 2 - 3i are (2, - 3). We can also represent this on the complex plan by drawing a vector from the origin to this coordinate.

To add them, we can simply transpose the w_bar vector to the head of the 2z vector and the resultant coordinates will be (12, -5).

Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.