filmov
tv
My Most Controversial Integral
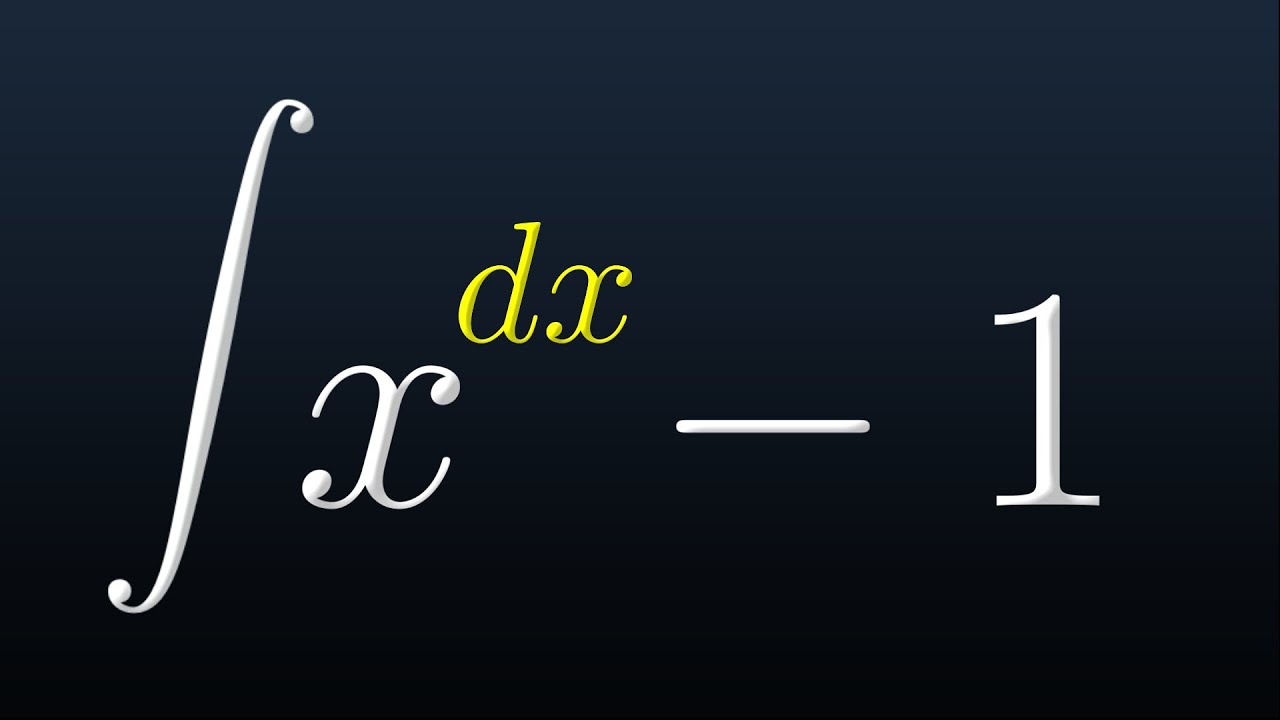
Показать описание
🙏Support me by becoming a channel member!
#math #brithemathguy #integral
This video was sponsored by Brilliant.
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
Комментарии