filmov
tv
Volume of a Frustum

Показать описание
Volume of the Frustum of a Cone. Here I calculate the volume of the frustum of a cone using the disk method from calculus. I also present a way of doing it without using any calculus, by using the formula for the volume of a cone. This is a very classical exercise in section 6.2 in Stewart's calculus textbook.
GCSE Maths - How to Find the Volume of a Frustum #114
Volume of a Frustum - Corbettmaths
Mensuration - Simplified volume of the Frustum
Another method of finding volume of a Frustum
Form 2 Maths .Volume of a Frustum
Volume of a Frustum | Grade 7-9 Series | GCSE Maths Tutor
How to find the volume of a Frustum - from a cone
Volume of a Frustum (Mensuration)
Volume of the frustum || Mensuration ||
Frustum of a Cone _ Volume _ Derivation _ Derivation of Volume of Frustum of a Cone _ Gautam Gautam
Volume of a frustum
Key Skill - Find the volume of a frustum of a cone.
Volume of a frustum | Surface areas and volumes | Class 10 (India) | Math
Volume | Frustum | Pyramid | Paper 2, 2023 Exam Question
VOLUME OF A FRUSTUM FROM A CONE
MENSURATION | Volume of the Frustum
GCE Volume of a Frustum (squares base pyramid) - Mensuration
Volume of a Frustum of a Pyramid from a Rectangular base
Volume of a Frustum Form Two
How to find the volume of a Frustum.
The Easiest Way | Calculate The Volume
VOLUME OF A FRUSTUM.
Why 1/3 in Volume of Frustum
7.2 HW#17: Volume of a frustum with square base of side 23, square top of side 9 and height 20
Комментарии
 0:03:52
0:03:52
 0:08:28
0:08:28
 0:09:25
0:09:25
 0:07:36
0:07:36
 0:07:39
0:07:39
 0:20:55
0:20:55
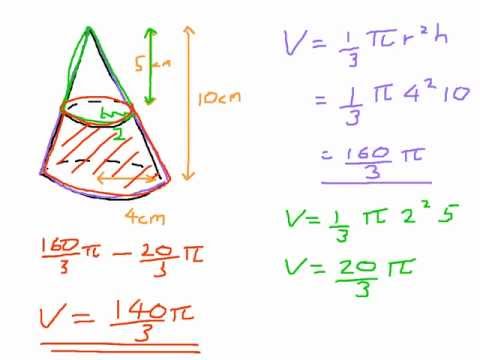 0:04:52
0:04:52
 0:10:05
0:10:05
 0:10:30
0:10:30
 0:07:08
0:07:08
 0:07:06
0:07:06
 0:03:46
0:03:46
 0:07:40
0:07:40
 0:08:26
0:08:26
 0:07:48
0:07:48
 0:06:33
0:06:33
 0:09:46
0:09:46
 0:09:22
0:09:22
 0:07:02
0:07:02
 0:05:54
0:05:54
 0:04:53
0:04:53
 0:05:12
0:05:12
 0:08:27
0:08:27
 0:23:21
0:23:21