filmov
tv
Proving sqrt(2) is irrational! (Classic Proof)
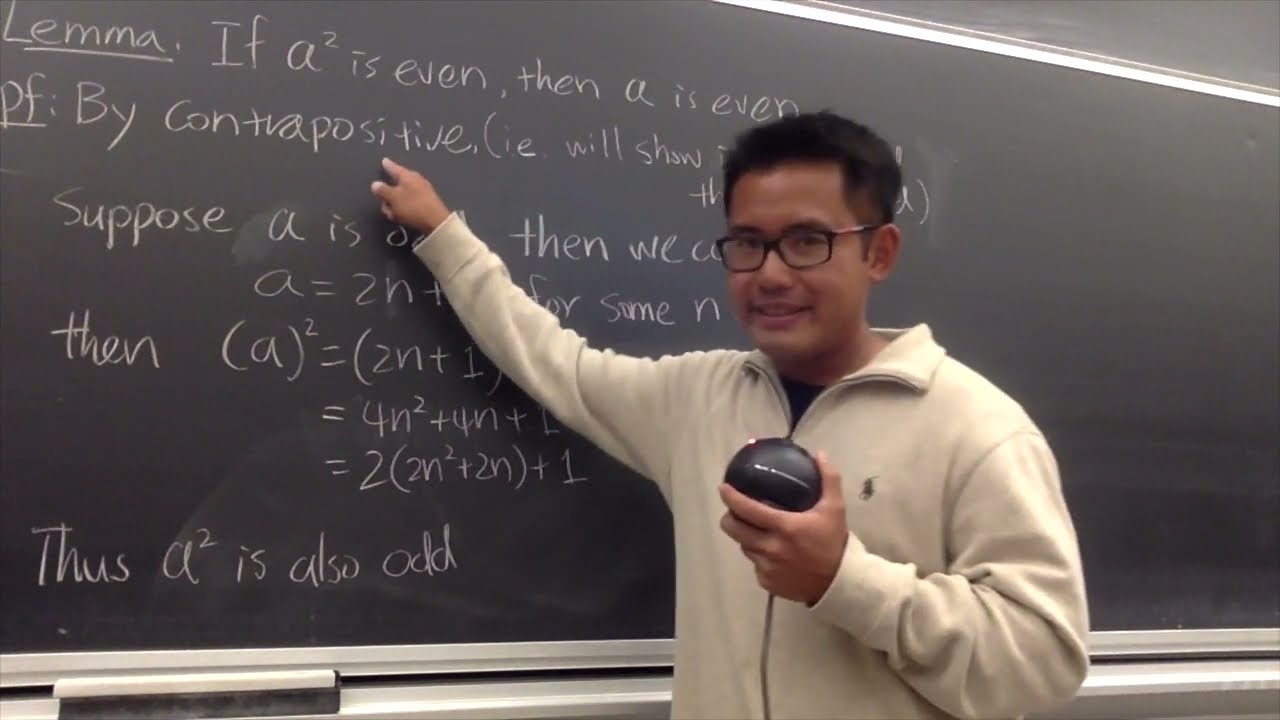
Показать описание
Here's the classic proof that square root of 2 is irrational.
Proof by contradiction!
blackpenredpen,
math for fun
Proof by contradiction!
blackpenredpen,
math for fun
Proving sqrt(2) is irrational! (Classic Proof)
Proof: Square Root of 2 is Irrational
Geometric proof of sqrt(2) is irrational, NON-classic method 1
The Most Beautiful Proof sqrt(2) is Irrational
Proof Square Root 2 is Irrational
Proof that the square root of 2 is irrational
Proof that square root of 2 is irrational | Algebra I | Khan Academy
Proving the square root of 2 is irrational
Root Two is Irrational Visually
A-Level Maths: A1-11 Proving √2 is Irrational
Geometric proof of sqrt(2) is irrational, NON-classic method 2
a better proof that √2 is irrational?
Proof: The Square Root of 2 is Irrational
Proof that the square root of 2 is irrational
Proof that the Square Root of 2 is Irrational
A neat proof that root 2 is irrational
Proof that the square root of 2 is irrational
Prove Root Two is Irrational: A Classic Proof by Contradiction
Sqrt 2 is irrational proof
Proof by Contradiction: Sqrt(2) is Irrational
Classic Proof that √2 is IRRATIONAL
The 5 Best Proofs that the Square Root of 2 is Irrational
A Calculational Proof :: The square root of 2 is irrational
Murdered Over a Math Proof?! Irrational Numbers and the Square Root of 2
Комментарии
 0:11:29
0:11:29
 0:04:02
0:04:02
 0:06:55
0:06:55
 0:14:47
0:14:47
 0:02:56
0:02:56
 0:05:30
0:05:30
 0:07:47
0:07:47
 0:04:13
0:04:13
 0:01:00
0:01:00
 0:06:43
0:06:43
 0:08:47
0:08:47
 0:00:53
0:00:53
 0:08:52
0:08:52
 0:06:10
0:06:10
 0:03:29
0:03:29
 0:05:19
0:05:19
 0:04:11
0:04:11
 0:07:30
0:07:30
 0:01:00
0:01:00
 0:11:17
0:11:17
 0:08:16
0:08:16
 0:04:57
0:04:57
 0:28:56
0:28:56
 0:10:09
0:10:09