filmov
tv
P If \( \alpha, \beta, \gamma, \delta \) are the roots of the equat...

Показать описание
P
If \( \alpha, \beta, \gamma, \delta \) are the roots of the equation \( x^{4}-\mathrm{Kx}^{3}+\mathrm{Kx}^{2}+\mathrm{Lx}+\mathrm{M}=0 \), where \( \mathrm{K}, \mathrm{L} \& \mathrm{M} \) are real numbers,
W then the minimum value of \( \alpha^{2}+\beta^{2}+\gamma^{2}+\delta^{2} \) is \( -\mathrm{n} \). Find the value of \( \mathrm{n} \).
If \( \alpha, \beta, \gamma, \delta \) are the roots of the equation \( x^{4}-\mathrm{Kx}^{3}+\mathrm{Kx}^{2}+\mathrm{Lx}+\mathrm{M}=0 \), where \( \mathrm{K}, \mathrm{L} \& \mathrm{M} \) are real numbers,
W then the minimum value of \( \alpha^{2}+\beta^{2}+\gamma^{2}+\delta^{2} \) is \( -\mathrm{n} \). Find the value of \( \mathrm{n} \).
 0:00:55
0:00:55
 0:01:36
0:01:36
 0:05:58
0:05:58
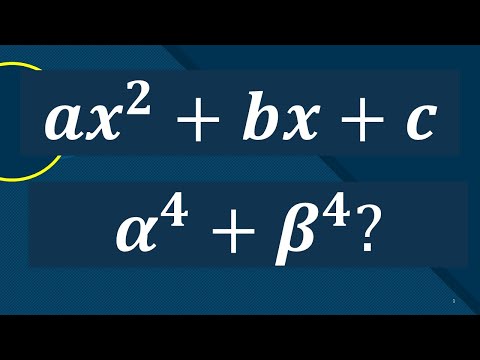 0:04:44
0:04:44
 0:04:48
0:04:48
 0:01:01
0:01:01
 0:03:10
0:03:10
 0:02:01
0:02:01
 0:03:07
0:03:07
 0:04:24
0:04:24
 0:03:25
0:03:25
 0:04:10
0:04:10
 0:04:14
0:04:14
 0:02:21
0:02:21
 0:05:12
0:05:12
 0:03:12
0:03:12
 0:10:32
0:10:32
 0:02:09
0:02:09
 0:08:30
0:08:30
 0:05:31
0:05:31
 0:01:13
0:01:13
 0:04:25
0:04:25
 0:02:18
0:02:18
 0:02:51
0:02:51