Algebra 1 Practice - Graph an Absolute Value Equation on a Coordinate Plane (Example 1)

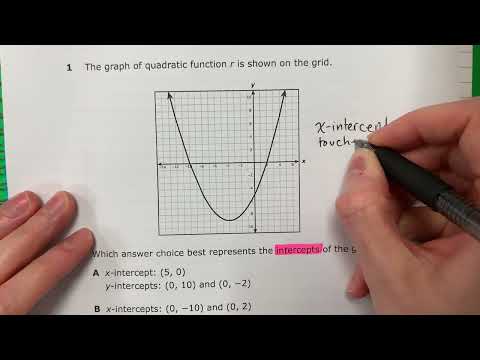
To graph an absolute value equation in the form \( y = a|x - b| + c \), follow these steps:

### 1. **Understand the Components**

- **Vertex:** The vertex of the graph is the point where the "V" shape begins. For the equation \( y = a|x - b| + c \), the vertex is \((b, c)\).
- **Slope:** The coefficient \(a\) determines the steepness of the "V" shape and whether it opens upward or downward.
- If \(a\) is positive, the graph opens upward.
- If \(a\) is negative, the graph opens downward.
- **Horizontal Shift:** The term \(b\) shifts the graph horizontally. The graph is shifted \(b\) units to the right if \(b\) is positive and to the left if \(b\) is negative.
- **Vertical Shift:** The term \(c\) shifts the graph vertically. The graph is shifted \(c\) units up if \(c\) is positive and down if \(c\) is negative.

### 2. **Plot the Vertex**

- Identify the vertex of the graph \((b, c)\) and plot this point on the coordinate plane.

### 3. **Determine the Direction of the "V" Shape**

- Check the value of \(a\):
- If \(a\) is positive, draw lines that slope upwards from the vertex.
- If \(a\) is negative, draw lines that slope downwards from the vertex.

### 4. **Find Additional Points**

1. **Select a Point to the Left and Right of the Vertex:**
- Choose a value for \(x\) on both sides of the vertex \(x = b\).
- Substitute these values into the equation \( y = a|x - b| + c \) to find the corresponding \(y\)-values.

2. **Calculate and Plot These Points:**
- For each selected \(x\), compute \( y \) and plot the resulting points.

### 5. **Draw the Graph**

- Connect the plotted points with straight lines to form the "V" shape.

**Example:**

For the equation \( y = 2|x - 1| - 3 \):

1. **Vertex:**
- The vertex is at \((1, -3)\). Plot this point.

2. **Direction:**
- The coefficient \(2\) is positive, so the "V" opens upward.

3. **Find Additional Points:**

- Choose \(x\) values to the left and right of \(x = 1\), for example \(x = 0\) and \(x = 2\):

- For \(x = 0\):
\[
y = 2|0 - 1| - 3
\]
\[
y = 2 \cdot 1 - 3
\]
\[
y = 2 - 3 = -1
\]
Plot the point \((0, -1)\).

- For \(x = 2\):
\[
y = 2|2 - 1| - 3
\]
\[
y = 2 \cdot 1 - 3
\]
\[
y = 2 - 3 = -1
\]
Plot the point \((2, -1)\).

4. **Draw the Graph:**
- Connect the vertex \((1, -3)\) to \((0, -1)\) and \((2, -1)\) with straight lines to form the "V" shape.

This method will allow you to graph any absolute value equation of the form \( y = a|x - b| + c \).

I have many informative videos for Pre-Algebra, Algebra 1, Algebra 2, Geometry, Pre-Calculus, and Calculus. Please check it out:

/ nickperich

Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa

#math #algebra #algebra2 #maths