Area of plane figures | rectangle/square/rhombus/parallelogram & trapezium

Area of quadrilaterals || rectangle & square & rhombus & parallelogram & trapezium
#Area of #quadrilaterals || #rectangle & #square & #rhombus & #parallelogram & #trapezium

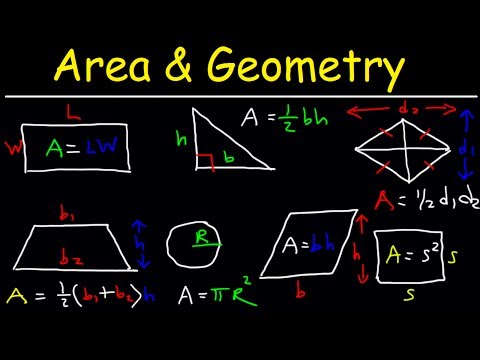
Area of Plane Shapes

Area is the size of a surface!
Learn more about Area, or try the Area Calculator.



Triangle
Area = ½ × b × h
b = base
h = vertical height

 



Square
Area = a2
a = length of side

 



Rectangle
Area = w × h
w = width
h = height

 



Parallelogram
Area = b × h
b = base
h = vertical height

 



Trapezoid (US)
Trapezium (UK)
Area = ½(a+b) × h
h = vertical height

 



Circle
Area = π × r2
r = radius

 



Ellipse
Area = πab

 



Sector
Area = ½ × r2 × θ
r = radius
θ = angle in radians


Note: h is at right angles to b

 

Example: What is the area of this rectangle?



The formula is:

Area = w × h
w = width
h = height

We know w = 5 and h = 3, so:

Area = 5 × 3 = 15

Example: What is the area of this circle?



Radius = r = 3

Area = π × r2  = π × 32  = π × (3 × 3)  = 3.14159... × 9  = 28.27 (to 2 decimal places)

Example: What is the area of this triangle?



Height = h = 12

Base = b = 20

Area = ½ × b × h = ½ × 20 × 12 = 120

 

A harder example:

Example: Sam cuts grass at $0.10 per square metre

How much does Sam earn cutting this area:



Let's break the area into two parts:



Part A is a square:

Area of A = a2 = 20m × 20m = 400m2

Part B is a triangle. Viewed sideways it has a base of 20m and a height of 14m.

Area of B = ½b × h = ½ × 20m × 14m = 140m2

So the total area is:

Area = Area of A + Area of B = 400m2 + 140m2 = 540m2

 

Sam earns $0.10 per square metre

Sam earns = $0.10 × 540m2 = $54

Area of Plane Figures

TABLE OF CONTENTS

When you try vacuum cleaning or brushing the floor of your room, do you consider how large your floor is? The floor of your room is a plane, hereafter, we shall learn how to calculate its size, also known as area.

What are plane figures?

Plane figures are two-dimensional surfaces that have no height or thickness.

Area of plane figures in maths

In Mathematics, problems on the area of plane figures can come in two ways. Firstly, you may just be given a plane shape that may be regular or irregular to determine its areas, such as finding the area of any polygon, circle or cross.

Regular plane figures

We have regular plane shapes when the interior angles and length of sides are equal. Examples of regular plane shapes are, for instance, a square, an equilateral triangle and a regular polygon (regular pentagon, regular hexagon, regular heptagon, regular octagon, etc.).

Irregular plane figures

Irregular plane figures occur when either the interior angles or the length of their sides are unequal. Examples of irregular plane figures are a rectangle, a parallelogram, a non-equilateral triangle (right, isosceles, scalene), irregular quadrilaterals, irregular pentagons, irregular hexagons, etc.

Triangles

A triangle is a 3-sided plane shape. The general formula used in calculating the area of a triangle is the product of half of its base and the height:.

Quadrilaterals

A quadrilateral is a 4-sided plane shape where the sum of their interior angles is equal to 360 degrees. There are several quadrilaterals, each has a formula for calculating its area.

Rectangle

A rectangle has all interior angles equal to 90 degrees and has its opposite sides equal.

Square

A square has all its interior angles equal to 90 degrees. Also, it has all its sides equal.

Rhombus

A rhombus is also called a diamond. It also has all its sides equal. Its opposite sides are parallel. Its area is calculated by multiplying its diagonals and dividing by 2.

Parallelogram

A parallelogram has its opposite sides parallel and equal. Its area is calculated by finding the product between the base and height of the parallelogram.

Kite

A kite has its adjacent sides equal the opposite interior angles are equal. The area of a kite is calculated by finding the product between its two diagonals and dividing them by 2.

Trapezium

A trapezium is a two-dimensional shape, which has two of its sides parallel usually called the bases. Its area is derived by getting the sum of bases and multiplying by half of its height.

Circle

A circle is a round plane figure whose boundary (circumference) consists of points equidistant from a fixed point called the center. A line that passes the circle from one end of the circle to another through its center is the diameter. A line drawn from any part of the circle's circumference to the center of the circle is the radius.