filmov
tv
Solving Exponential Equation @KasyannoEZMath
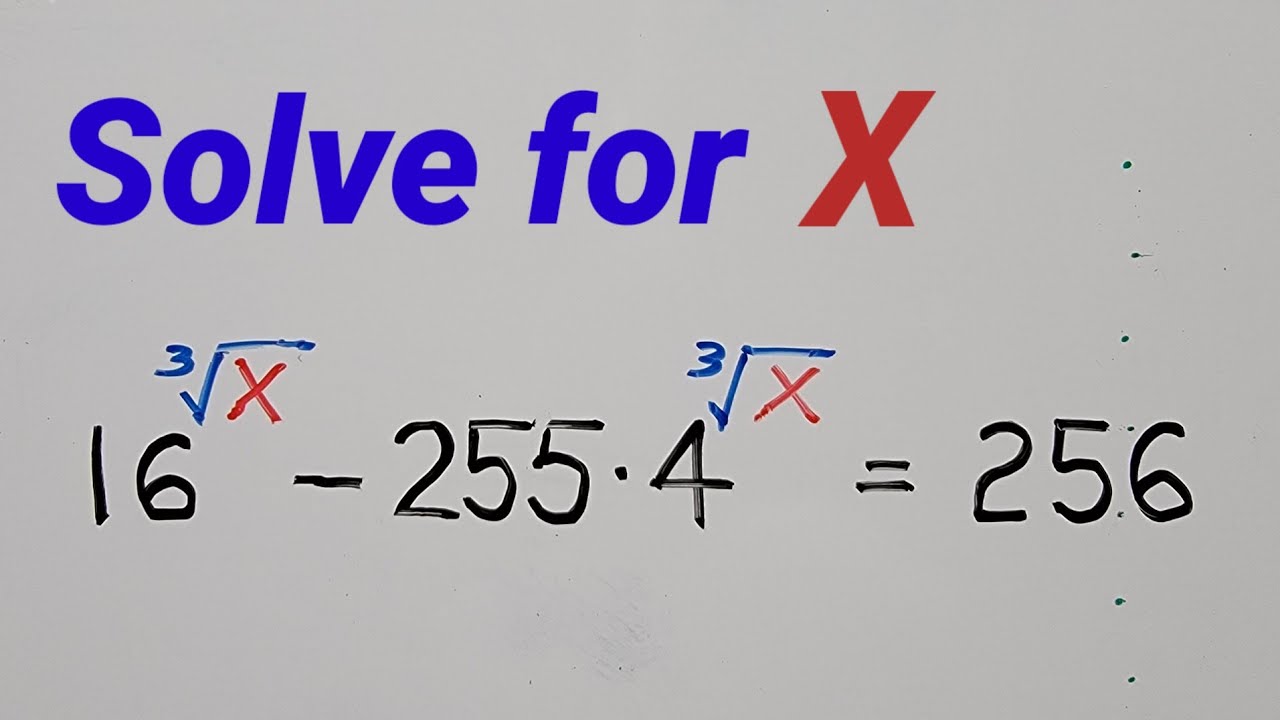
Показать описание
This tutorial video explains how to solve the given exponential equation.
For those new to my channel, please subscribe to my channel @KasyannoEZMath for more videos. Happy learning!
For those new to my channel, please subscribe to my channel @KasyannoEZMath for more videos. Happy learning!
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation in Two Ways @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
How to Solve this Exponential Equation @KasyannoEZMath
How to Solve This Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Solving Exponential Equation @KasyannoEZMath
Комментарии
 0:12:32
0:12:32
 0:11:36
0:11:36
 0:14:19
0:14:19
 0:13:23
0:13:23
 0:00:58
0:00:58
 0:00:59
0:00:59
 0:14:35
0:14:35
 0:15:24
0:15:24
 0:13:30
0:13:30
 0:08:32
0:08:32
 0:06:30
0:06:30
 0:14:42
0:14:42
 0:06:22
0:06:22
 0:11:33
0:11:33
 0:07:52
0:07:52
 0:08:54
0:08:54
 0:06:48
0:06:48
 0:13:14
0:13:14
 0:16:58
0:16:58
 0:00:58
0:00:58
 0:00:58
0:00:58
 0:09:13
0:09:13
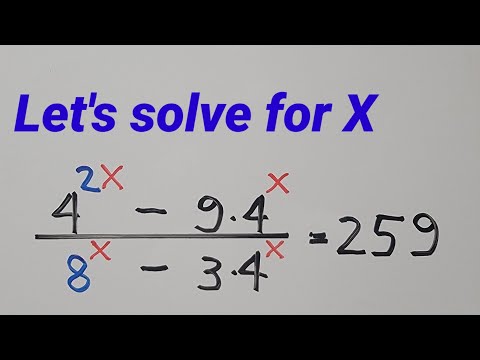 0:09:55
0:09:55
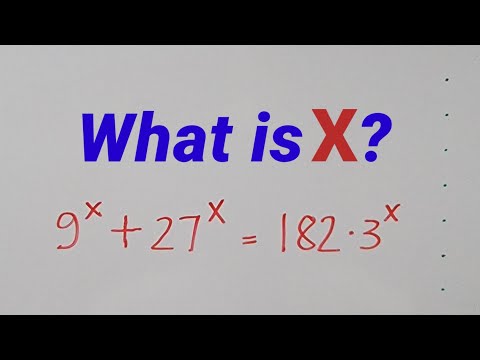 0:19:42
0:19:42