filmov
tv
Relationship between roots and coefficients for 4th Order Polynomials

Показать описание
If the equation ax^4 + bx^3 + cx^2 + dx+ e = 0 has the roots alpha α, beta β, gamma ɣ, and delta δ, then was are the relationships between these roots and the coefficients a, b, c and d? We find out in this video and we apply these to the following example:
We solve for α, β, ɣ, and δ given the equation x^4 - 2x^3 +4x^2 +6x - 21 = 0 and α + β = 0.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
We solve for α, β, ɣ, and δ given the equation x^4 - 2x^3 +4x^2 +6x - 21 = 0 and α + β = 0.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
Polynomial Roots and Coefficients (1 of 5: Relationship between roots and coefficients of cubics)
Relation between coefficients and roots of a quadratic equation (1/2) | Polynomial | Math | KA
Relationship between the Roots and the Coefficients (Part 1)
Polynomial Roots and Coefficients (2 of 5: Relationship of roots and coefficients in a Quartic)
HSC 4U Maths: Polynomials - Relationship between roots and coefficients
QUADRATIC EQUATIONS 02 | Relation Between Roots & Coefficients | Math | Pure English | Class 11t...
The Relationship Between the Coefficient and the Roots of Quadratic Equations | Grade 9
Relation Between Roots and Coefficients of Quadratic Equation | Math Dot Com
2022 past paper | MAT livestream 2024
Relation Between Roots and Coefficients - Theory of Equations - IIT JEE Mathematics Video Lectures
Relation of Roots with Coefficients : Quadratic Equations | Learn with BYJU'S
Maths: Relation between The Roots and Coefficients in Quadratic Equation.
Relationship Between Roots and Coefficients of Quadratic Equation | Sum and Product of Roots
Theory of Equation | Relation Between Roots & Coefficients | Examples
Relationship between roots and coefficients for 3rd Order Polynomials
Higher Degree Polynomial Equation : Relations Between Roots & Coefficients | Theory of Equation...
quadratic equation: relation between roots and coefficients
How to derive formulas of the roots of Quadratic Equations
Coefficients and Roots of Polynomials 1
Relation between Roots and Coefficients of Quadratic Equations Ex 2.7
Relation between roots and coefficients # algebra # TAM1A # SM21A
Relationship between coefficients and roots of quadratic equations
Mathematics-1st-Year-Ch-04-Relation-Between-Roots-and-Coefficients-of-Quadratic-Equation-Urdu|Hindi
Relation Between Roots & Coefficients of Quadratic Equation (Semi-English)
Комментарии
 0:10:17
0:10:17
 0:04:52
0:04:52
 0:12:15
0:12:15
 0:04:54
0:04:54
 0:11:02
0:11:02
 0:49:42
0:49:42
 0:15:02
0:15:02
 0:09:01
0:09:01
 2:04:14
2:04:14
 0:07:20
0:07:20
 0:20:05
0:20:05
 0:25:21
0:25:21
 0:11:04
0:11:04
 0:22:20
0:22:20
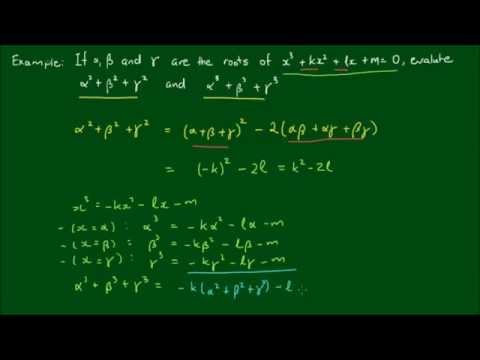 0:08:39
0:08:39
 0:20:11
0:20:11
 0:05:14
0:05:14
 0:25:54
0:25:54
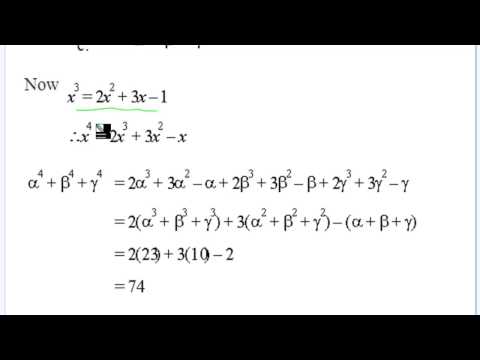 0:10:00
0:10:00
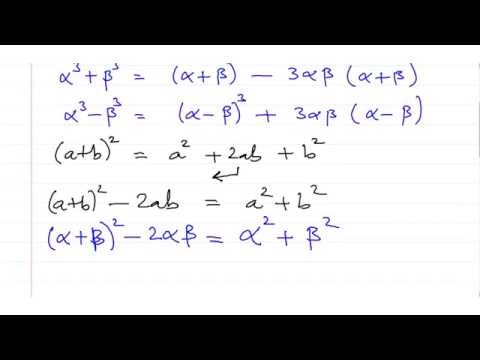 0:21:46
0:21:46
 0:17:16
0:17:16
 0:20:05
0:20:05
 0:10:11
0:10:11
 0:18:04
0:18:04