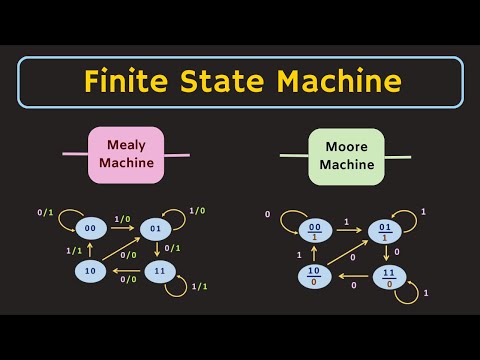
Finite State Machines (FSM)

Introduction: What are finite state machines?

A state machine is a model of a system with discrete dynamics that at each reaction maps valuations of the inputs to valuations of the outputs, where the map may depend on its current state. A finite-state machine (FSM) is a state machine where the set States of possible states is finite.

Transitions

Transitions between states govern the discrete dynamics of the state machine and the mapping of input valuations to output valuations. A transition is represented as a curved arrow between 2 states. A transition may also start and end at the same state. That is called a self transition. Transition between states is labeled with guard and action pair.
A guard is a boolean valued expression that evaluates to true when the transition should be taken.
An action is an assignment of values to output ports when a transition is taken.

Lets look an example: “A model of a thermostat with hysteresis”
When a temperature has fallen below 18 degrees, heater gets turned on, and the state is transitioned from cooling to heating. When a temperature has reached over 22 degrees, heater gets turned off and the state of a system is transitioned form heating to cooling. By that simple finite state machine, you can keep your room temperature near desired temperature.

When a reaction occurs

A transition can be either time triggered or event triggered
Time triggered means that it can react at regular time intervals. Event triggered means that it can react when for example a temperature input is provided.
The environment determines when the machine reacts. Lets focus on what the machine does when it reacts.

When a reaction occurs, the inputs will have a valuation and the state machine will assign a valuation to the output ports.
If no guard on any transition out of the current state evaluates to true, then the machine will remain in the same state.

If inputs and outputs are all absent and the machine does not change its state, then it's called a stuttering reaction. That results in no changes to the system.

A major advantage of finite-state machines is that they define all possible behaviors.

Update functions

The graphical notation for finite-state machines proves to be inconvenient for larger systems. That's when a mathematical models of the dynamics of the state machine is used.

In such mathematical notation, a finite-state machine is a five-tuple where:
States is a finite set of states; inputs is a set of input valuations; outputs is a set of output valuations; update is an update function, mapping a state and an input valuation to a next state and an output valuation; and initial states defines a machines starting state.
The term transition function is often used in place of update function.

Lets look an example of a mathematical notation of a counting machine
The machine has states 0, 1, 2, 3. Inputs are up and down as buttons that can have values of present and absent. An only output is a count of a counting machine that can have values 0, 1, 2, 3. Let the counter start with a state 0.
The dynamics of the state machine are given by the following equation: (s(n+1),y(n))=update(s(n),x(n)) where S is a state, Y is output and X is input.

Determinacy and Receptivness

State machines can have two important properties: determinancy and receptiveness.
A state machine is deterministic if, for each state, there is at most one transition enabled by each input value.

A state machine is receptive if, for each state, there is at least one transition possible on each input symbol.

If a state machine is both deterministic and receptive, for every state, there is exactly one transition possible on each input value.