Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 14.2 - Erdos Renyi Random Graphs

Jure Leskovec
Computer Science, PhD

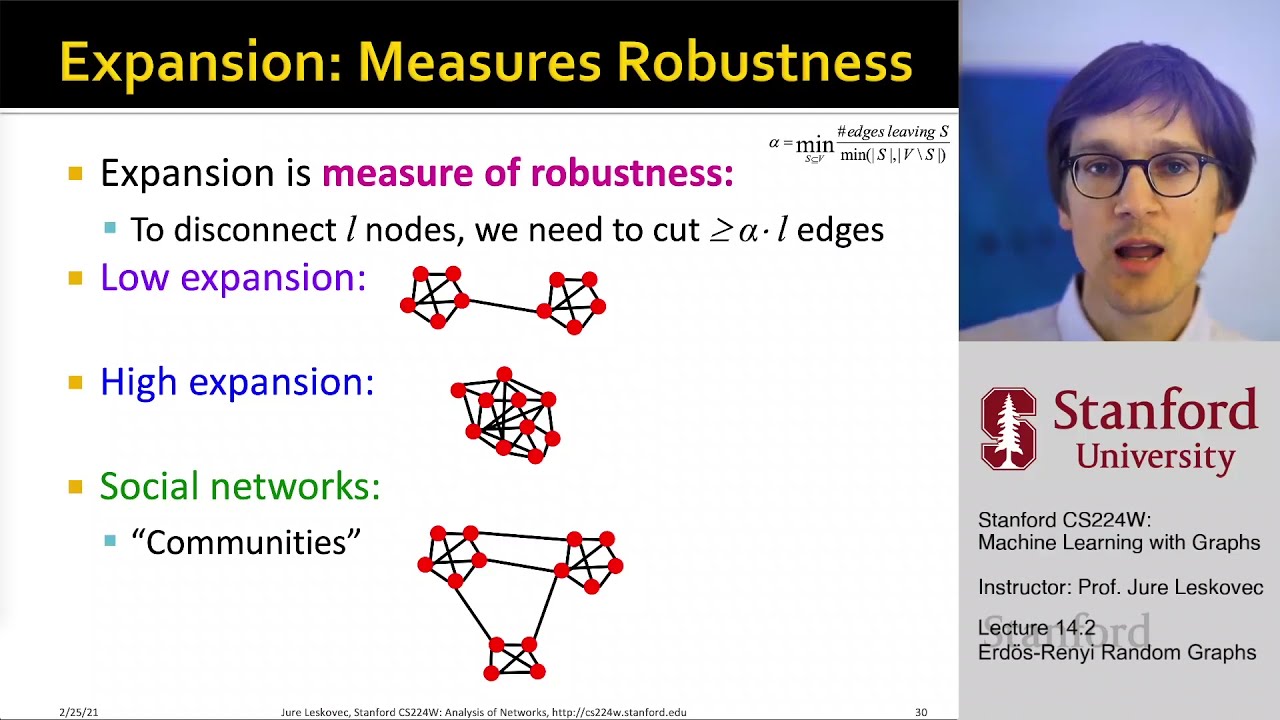
We introduce the simplest model for graph generation, Erdös-Renyi graph (E-R graphs, Gnp graphs). The Gnp random graphs are undirected graphs over n nodes, where each edge appears i.i.d. with probability p. We analyze ER graphs using the graph statistics we have introduced. Gnp graphs have binomial degree distribution. Gnp graphs have very small clustering coefficient. Graph structure of Gnp changes as p changes. To measure the path length of Gnp graphs, we introduce the nodtion of expansion, and derive that the shortest path length of Gnp graphs follows O(log n).

To follow along with the course schedule and syllabus, visit:

0:00 Introduction
0:33 Simplest Model of Graphs
1:50 Random Graph Model Gmp
2:19 Properties of Gmp
3:11 Degree Distribution of G
5:00 Clustering Coefficient of me Remember: C
7:03 Connected Components of G.mp . Graph structure of Gasp changes
8:29 GP Simulation Experiment
9:43 Def: Expansion
11:05 Expansion: Measures Robustness
12:42 Expansion: Random Graphs
15:01 Shortest Path of Go
15:31 Back to MSN vs. Gmp
18:38 Real Networks vs. G.

#machinelearning #machinelearningcourse

[evau]

could anyone find the slides associate with this lecture or find the lectures associated with the topics for the Deep generative models in the slides?