filmov
tv
Warum ist 0! = 1 und WTF ist eigentlich Fakultät?! #Shorts

Показать описание
Warum ist 0! gleich 1? Interessantes und Wissenswertes, Mathematik, Mathe by Daniel Jung
X^0 - Warum gibt hoch 0 immer 1?
Warum ist x hoch 0 gleich 1?🤯🤔
Potenzrechnung: Warum ist x hoch 0 = 1 | erklärt von Lehrerschmidt
Why is 0! = 1?
Bits und Bytes: Binärziffern 0 und 1 - Arithmetik in Computern 1
Why do numbers to the power of 0 equal 1?
Warum ist a hoch 0 = 1 ? #mathematik #lehramt #studium
Tosin Adarabioyo Goal, Espérance Tunis vs Chelsea 0-1 Highlights, FIFA Club World Cup 2025
Was bringt ein 1,0 Abitur überhaupt?!
GRAMMARBOX: if-clauses 0/1 | Konditionalsätze Typ 0 / 1 | Bedingungssätze 0/ 1 😎 (no hand)
nur 0,1% können das in fortnite
What is RAID 0, 1, 5, & 10?
0/1 Knapsack problem | Dynamic Programming
🚨 PENAL Y GOL Álex Valera | Atlético Grau 0-1 Universitario | Apertura 2025 | Liga 1 Perú
zero factorial, why 0! should be 1, 4 reasons
42 DINGE in MINECRAFT die nur 0,1% DER SPIELER wissen!
Meinung nach 0,1 Sekunden geändert😂
4.5 0/1 Knapsack - Two Methods - Dynamic Programming
0-1 Binary Constraints | Integer Linear Programming | Examples - Part 1
Integer Linear Programming - Binary (0-1) Variables 1, Fixed Cost
SO schaffst du 1,0 Noten: Schneller Auswendig Lernen #ytshorts
1,0 Abitur bekommen
Paluten REAGIERT auf 42 DINGE in MINECRAFT die nur 0,1% DER SPIELER wissen!
Комментарии
 0:02:30
0:02:30
 0:03:06
0:03:06
 0:00:46
0:00:46
 0:03:07
0:03:07
 0:06:05
0:06:05
 0:04:56
0:04:56
 0:05:58
0:05:58
 0:01:00
0:01:00
 0:00:53
0:00:53
 0:00:53
0:00:53
 0:05:57
0:05:57
 0:00:25
0:00:25
 0:05:04
0:05:04
 0:13:29
0:13:29
 0:03:13
0:03:13
 0:12:58
0:12:58
 0:14:13
0:14:13
 0:00:14
0:00:14
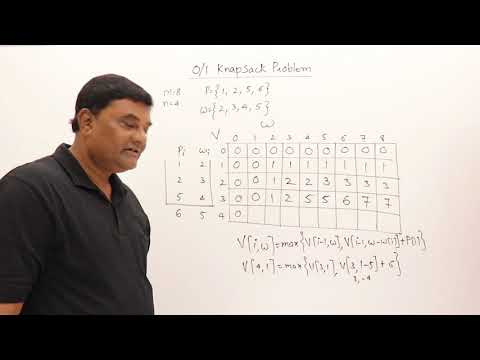 0:28:24
0:28:24
 0:04:01
0:04:01
 0:06:00
0:06:00
 0:00:18
0:00:18
 0:00:18
0:00:18
 0:15:59
0:15:59