Abst Alg 11: Orders of Permutations, Isomorphism S3 to D3, Elements & Subgrps of Symmetric Group S4

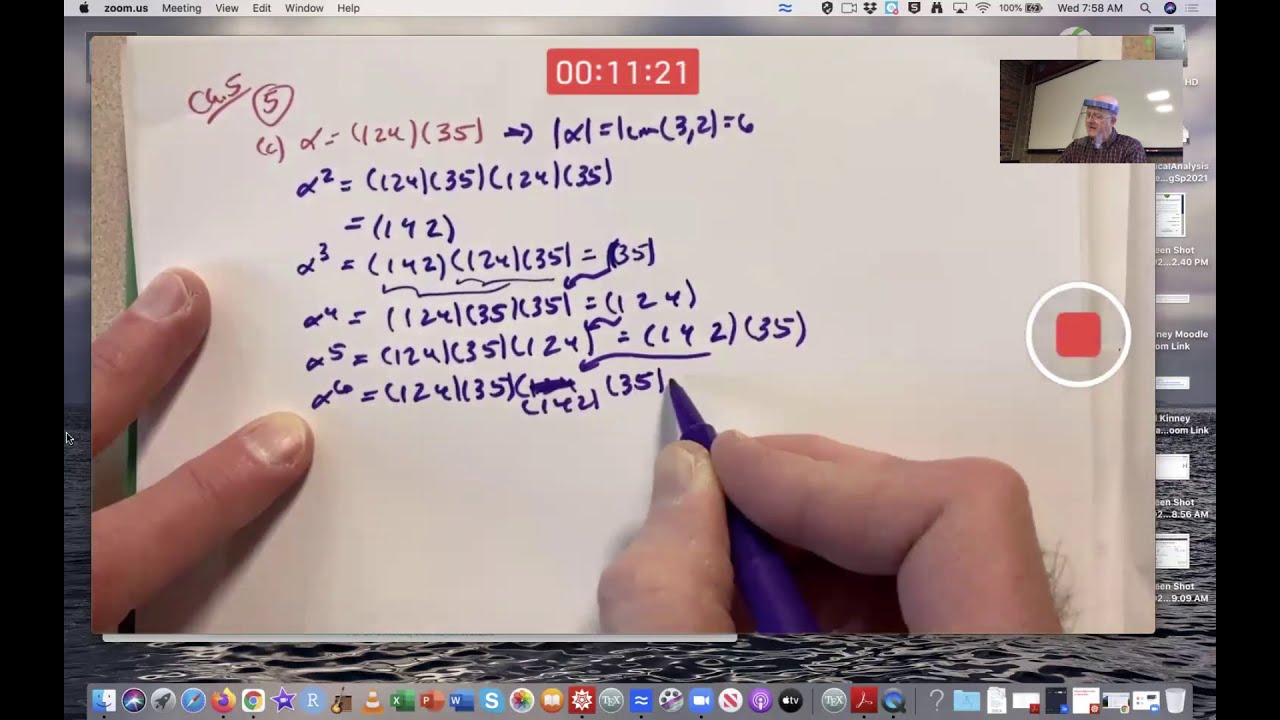
Find orders of permutations in disjoint cycle form as the lcm of the lengths of the cycles (least common multiple of the cycle lengths). Construct an isomorphism from the symmetric group S3 of all permutations on a set of three objects to the dihedral group of symmetries of an equilateral triangle D3. List out the elements of order 1, 2, 3, and 4 in the symmetric group S4 of all permutations on a set of four objects. Also find subgroups of order 1, 2, 3, 4, 6, 8, 12, and 24 of the symmetric group S4. The subgroups found of orders 1, 2, 3, and 4 are cyclic (though there are non-cyclic groups of order 4). The subgroups of order 6 are isomorphic to S3. The subgroups of order 8 are isomorphic to D4, the symmetries of a square. And the subgroup of order 12 is called the alternating group A4 of even permutations in S4 (which can be written as a product of an even number of two cycles (an even number of transpositions).

Abstract Algebra, Class 11, 24 February 2021.

Abstract Algebra Screencast of Class 11 on 24 February, 2021.

#symmetricgroup #isomorphism #isomorphicgroups

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.