filmov
tv
Solving by Graphing and Using Algebra

Показать описание
Solving Systems of Equations By Graphing
Learn how to solve a system of equations by graphing
Solving a linear system of two equations by graphing
Solving System of Linear Equations by Graphing - Math Teacher Gon
How to Solve a System of Equations using the Graphing Method - Fast & Easy Explanation
Solving a system of inequalities by graphing and shading
Solving Systems of Equations by Graphing, Substitution, and Elimination
Algebra - Solving Linear Equations by using the Graphing Method 1/2
DILR-Pie chart #ytshort #youtubeshorts #shorts #viralshorts #catexam2024
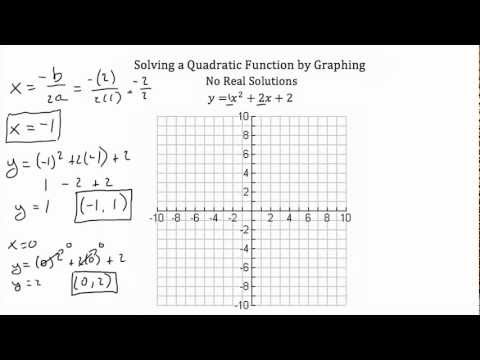
Solving Quadratic Equations by Graphing
Solving Systems of Linear Equations by Graphing
Solving Equations and Inequalities by Graphing
Algebra Basics: Graphing On The Coordinate Plane - Math Antics
How to solve a system of equations by graphing both equations
Solve a System by Graphing, Substitution, Elimination
Solve a system of equations by graphing in standard form
Graphs of linear equations | Linear equations and functions | 8th grade | Khan Academy
Algebra - Solving Linear Equations by using the Graphing Method 2/2
How to solve a system of equations by graphing
Solving linear systems by graphing | Systems of equations | 8th grade | Khan Academy
Graphing Equations in Standard Form
How do find the x and y intercepts and graph
Graphing in Algebra: Ordered Pairs and the Coordinate Plane
Graphing a linear equation by rewriting from standard form to slope intercept form
Комментарии
 0:05:15
0:05:15
 0:04:47
0:04:47
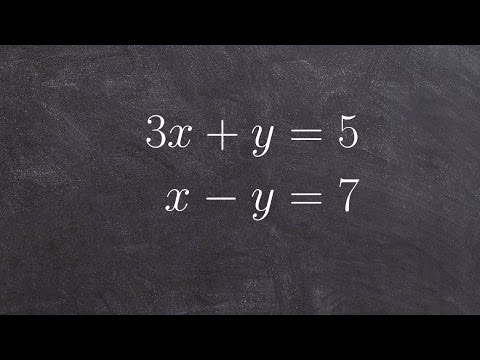 0:05:22
0:05:22
 0:10:47
0:10:47
 0:07:59
0:07:59
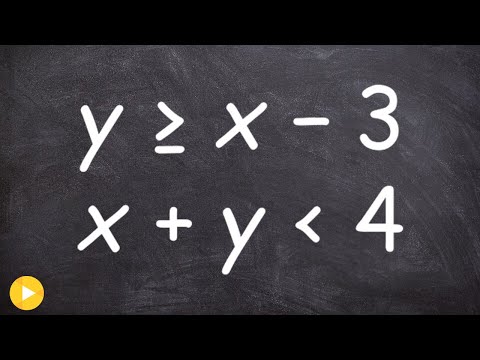 0:04:10
0:04:10
 0:09:00
0:09:00
 0:05:06
0:05:06
 0:00:50
0:00:50
 0:12:07
0:12:07
 0:02:55
0:02:55
 0:05:15
0:05:15
 0:10:14
0:10:14
 0:07:26
0:07:26
 0:13:48
0:13:48
 0:02:51
0:02:51
 0:13:10
0:13:10
 0:03:32
0:03:32
 0:04:45
0:04:45
 0:08:30
0:08:30
 0:04:47
0:04:47
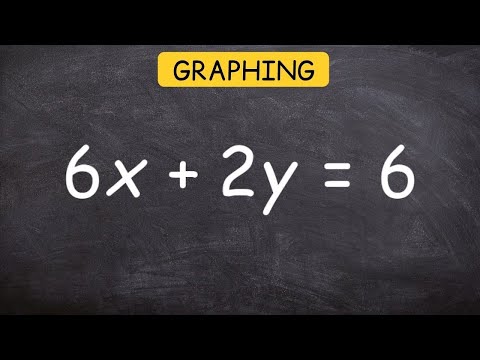 0:04:55
0:04:55
 0:06:56
0:06:56
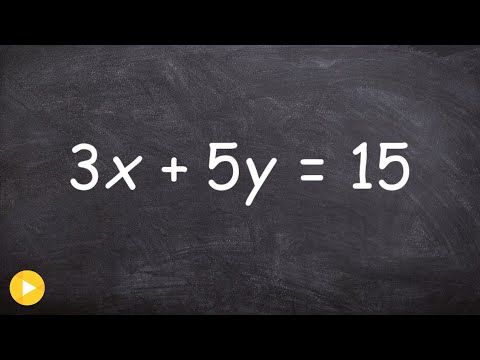 0:04:53
0:04:53