filmov
tv
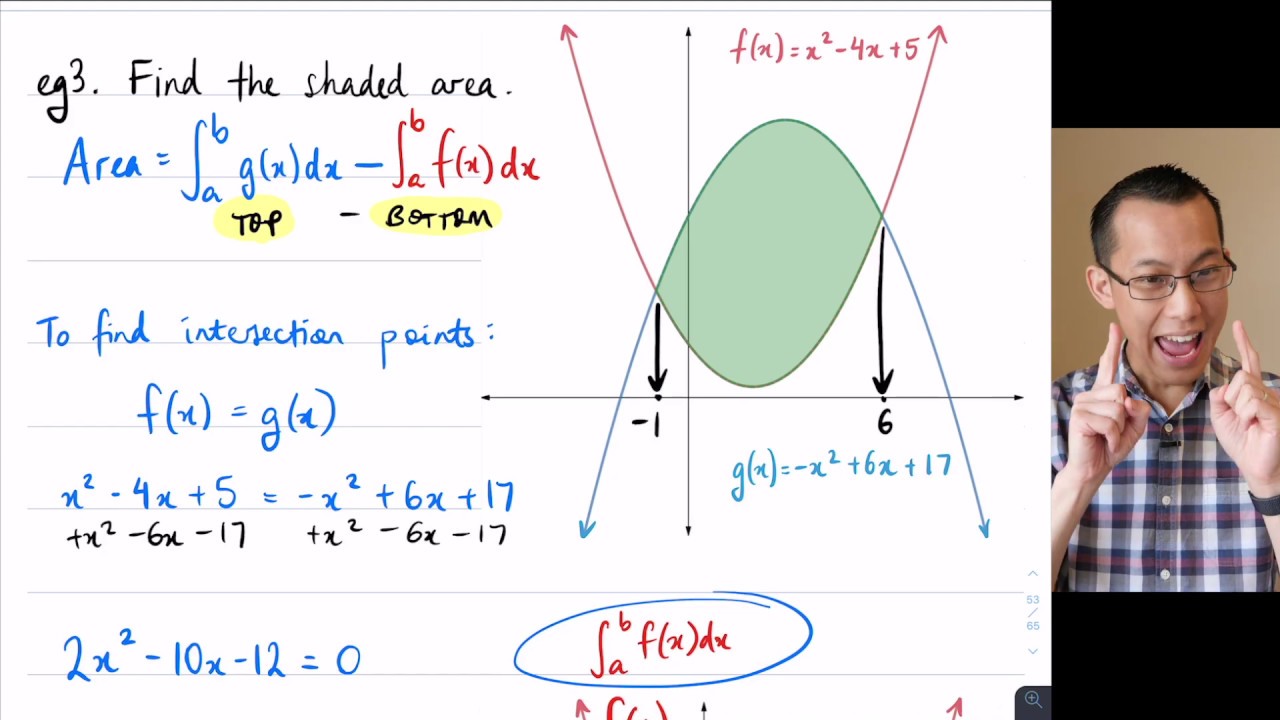
Areas Between Curves (3 of 3: What about beneath the x-axis?)
Показать описание
Finding The Area Bounded By Three Curves Using Definite Integrals - Calculus
Area of a Region Bounded by 3 Curves (Calculus)
Areas Between Curves (3 of 3: What about beneath the x-axis?)
Area between curves with multiple boundaries
Area Between Curves - 3
Area Between Two Curves
📚 How to find the area between two curves using integrals (Part 3)
Finding the Area Between Two Curves by Integration
Solving Area Between Curves Maths Methods Problem (PART2)
Area Between Curves Example 3 (KristaKingMath)
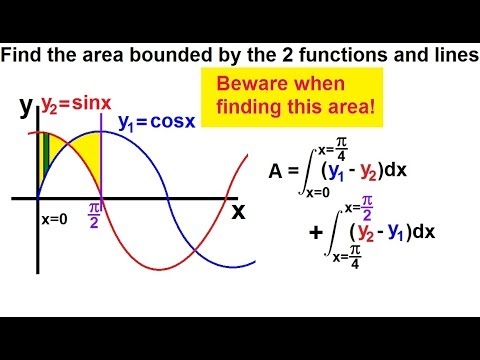
Calculus 2 - Integration: Finding the Area Between Curves (3 of 22) Ex. 3: y=sinx, y=cosx BEWARE!
Areas Between Curves (2 of 3: Evaluating the integrals)
Calculus 2 - Integration: Finding the Area Between Curves (19 of 22) 3 Curves
Area Between TWO Curves (integration) #calculus #mathchallenge #mathtricks #calculushelp
Areas Involving Multiple Curves (3 of 4: Finding Similarities between translated areas)
[Calculus] Area Between Curves for y=f(x)
Areas Between Curves (1 of 3: Establishing 'top' minus 'bottom')
Finding Area Between Curves
Calculus 2 - Integration: Finding the Area Between Curves (9 of 22) Example 8: Method 2 of 3
Curves with Multiple Crossings (1 of 5: Locating the boundaries)
Area between curves
Part 3, Area Between two curves,
Calculus 2 - Integration: Finding the Area Between Curves (10 of 22) Example 8: Method 3 of 3
Area Between Two Curves Example 3
Комментарии
 0:12:57
0:12:57
 0:07:35
0:07:35
 0:09:11
0:09:11
 0:06:54
0:06:54
 0:10:23
0:10:23
 0:48:59
0:48:59
 0:07:53
0:07:53
 0:07:52
0:07:52
 0:01:01
0:01:01
 0:11:43
0:11:43
 0:08:43
0:08:43
 0:12:38
0:12:38
 0:06:54
0:06:54
 0:00:53
0:00:53
 0:07:46
0:07:46
![[Calculus] Area Between](https://i.ytimg.com/vi/mABUT6PQgLo/hqdefault.jpg) 0:17:07
0:17:07
 0:08:09
0:08:09
 0:06:35
0:06:35
 0:03:21
0:03:21
 0:08:24
0:08:24
 0:04:09
0:04:09
 0:08:04
0:08:04
 0:02:45
0:02:45
 0:02:52
0:02:52