filmov
tv
Solve trigonometric equation: sin x + sin 2x + sin 3x = 0. Math Olympiad Algebra Problem.

Показать описание
How to solve trigonometric equation: sin x + sin 2x + sin 3x = 0. Challenging Algebra Problem. Math Olympiad Algebra Problem. Step-by-step tutorial by Fun with Maths.
Solving Trigonometric Equations: sin x = 1/2
Solve the Trig equation sin x = 1/2. Give a general formula and list six solutions
Solve the Trig equation sin x - sqrt(3) cos x = 1 on the interval [0, 2pi)
Solving Trigonometric Equations By Finding All Solutions
How To Solve Trigonometric Equations With Multiple Angles - Trigonometry
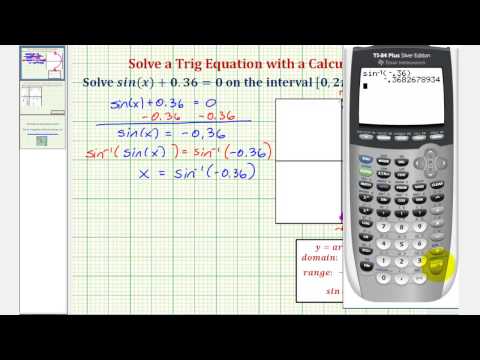
Ex: Solve a Trigonometric Equation Using a Calculator (sin(x)=-0.36)
Solve the Trigonometric Equation 5*sin(x) - 6 = 0
Solve sin=2/5 Trigonometric equation
TRIGONOMETRY in 1 Shot | All Concepts Covered | JEE Mains and Advanced | JEE 2025
Solve sin(x+30)=2 cos(x+45),[0°,360°] Trigonometric Equation
Solve the Trig equation sin x + cos x = 1 over the interval [0, 2pi)
Ex: Solve sin(x)=a Using a Calculator (positive a)
Find General Solution for Trig Equation sin x equals negative cos x
A-Level Maths: E7-21 [Trig Equations: Solve sin(x + 65) = 0.7 between 0 and 360 degrees]
Steps to Solve Linear Trigonometric Equation sinx + sqrt 3 cosx = 0
Sine equation algebraic solution set | Trigonometry | Precalculus | Khan Academy
Solve the trig equation sin 2x - sin x = 0 in [0,2pi)
Solve Trigonometric Equation sin x + cos x = 1 Extraneous Roots Q10
Ex: Solve Trig Equation: sin(x) = cos(x)
Solve the equation 2sin 3x - sin x = 0
Solving Trigonometric Equations
How to Solve cos(x) + sin(2x) = 0 (Trigonometric Equations)
Solve Trig Equation by Factoring: 2sin^2(x)-sin(x)-1=0 (Radians)
General Solution for sin x = sin A | Trigonometric Equations | JEE 2023 Concept | Maths
Комментарии
 0:08:07
0:08:07
 0:03:42
0:03:42
 0:06:06
0:06:06
 0:11:49
0:11:49
 0:11:34
0:11:34
 0:06:47
0:06:47
 0:01:15
0:01:15
 0:04:04
0:04:04
 2:54:28
2:54:28
![Solve sin(x+30)=2 cos(x+45),[0°,360°]](https://i.ytimg.com/vi/_VZ-_Me65l4/hqdefault.jpg) 0:07:20
0:07:20
 0:04:59
0:04:59
 0:03:13
0:03:13
 0:06:24
0:06:24
 0:06:48
0:06:48
 0:07:37
0:07:37
 0:05:36
0:05:36
 0:00:48
0:00:48
 0:07:51
0:07:51
 0:04:30
0:04:30
 0:08:59
0:08:59
 0:15:22
0:15:22
 0:04:54
0:04:54
 0:04:42
0:04:42
 0:05:35
0:05:35