filmov
tv
Given an equation find the vertices, center and foci of hyperbola
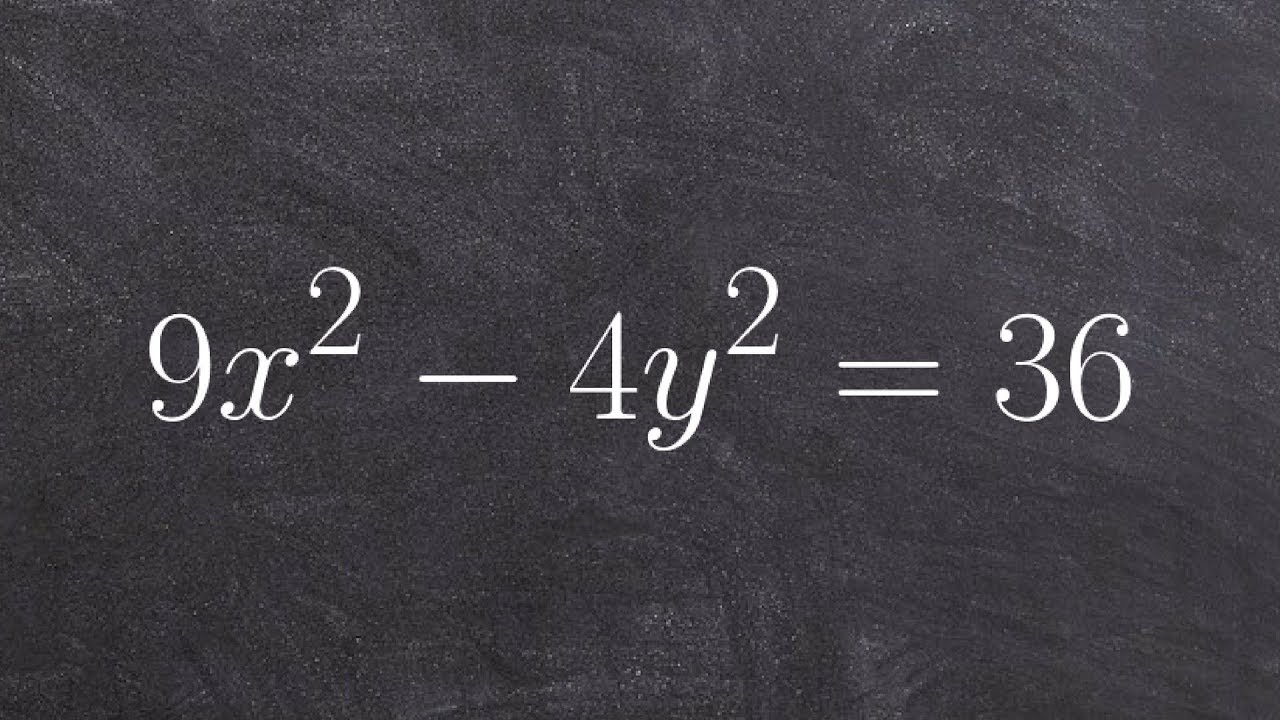
Показать описание
Learn how to graph hyperbolas. To graph a hyperbola from the equation, we first express the equation in the standard form, that is in the form: (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1 for horizontal hyperbola or (y - k)^2 / a^2 - (x - h)^2 / b^2 = 1 for vertical hyperbola.
Next, we identify the characteristics of the given hyperbola. 'a' (the distance from the center to the vertices) is the square root of the first denominator and 'b' (the distance from the center to the covertices) is the square root of the second denominator. 'c' (the distance from the center to the foci) is obtained by taking the square root of the sum of a^2 and b^2. Using these characteristics of the hyperbola, we can graph the asymptotes of the hyperbola and hence graph the hyperbola.
Note that a hyperbola is vertical when it is facing up and down and is horizontal when it is facing right and left.
#conicsections #hyperbolaconicsections
#conicsections #hyperbolaconicsections
#conicsections #hyperbolaconicsections
Next, we identify the characteristics of the given hyperbola. 'a' (the distance from the center to the vertices) is the square root of the first denominator and 'b' (the distance from the center to the covertices) is the square root of the second denominator. 'c' (the distance from the center to the foci) is obtained by taking the square root of the sum of a^2 and b^2. Using these characteristics of the hyperbola, we can graph the asymptotes of the hyperbola and hence graph the hyperbola.
Note that a hyperbola is vertical when it is facing up and down and is horizontal when it is facing right and left.
#conicsections #hyperbolaconicsections
#conicsections #hyperbolaconicsections
#conicsections #hyperbolaconicsections
How To Find The Equation of a Line Given Two Points
How To Find The Equation of a Line From a Graph | Algebra
Finding the equation of a straight line given the gradient and a point
GCSE Maths - Finding the Equation of a Straight Line From 2 Sets of Coordinates #69
How To Find The Equation of a Quadratic Function From a Graph
How to find the equation of a line given two points
How to Find the Slope from an Equation
Find the equation of a line through two points using slope intercept form
Linear Functions: Writing Equations of Lines (Part 2)
How To Write The Equation of a Line Given The Slope and a Point | Algebra
Find The Equation of A Line Given Two Points - Understand In 10 Minutes
Equation of a Line Given Two Points
GCSE Maths - How to Find the Equation of a Straight Line (y = mx + c) #68
How To Find The Equation of a Plane Given Three Points
Finding Ordered Pairs that Satisfy a Given Equation
Write the equation of a line given a slope and a point the line runs through
Find Equation of Line Perpendicular to a Line Through a Given Point
How to find the x and y intercept from an equation
Finding the Equation of a Line Given Slope and a Point - Point - Slope Form
Determine the slope and y intercept from an equation in standard form
How To Write a Linear Equation From a Function Table | Algebra
Given the equation of a circle find the center and radius
Find the Equation of a Circle Given Endpoints of Diameter
How To Find The Vector Equation of a Line and Symmetric & Parametric Equations
Комментарии
 0:07:38
0:07:38
 0:10:05
0:10:05
 0:01:54
0:01:54
 0:06:07
0:06:07
 0:09:35
0:09:35
 0:04:41
0:04:41
 0:02:02
0:02:02
 0:05:04
0:05:04
 0:09:12
0:09:12
 0:08:32
0:08:32
 0:11:26
0:11:26
 0:05:22
0:05:22
 0:04:28
0:04:28
 0:06:56
0:06:56
 0:02:53
0:02:53
 0:04:37
0:04:37
 0:02:26
0:02:26
 0:03:32
0:03:32
 0:08:28
0:08:28
 0:02:44
0:02:44
 0:14:51
0:14:51
 0:02:39
0:02:39
 0:02:01
0:02:01
 0:11:37
0:11:37