Understanding the Time Complexity of Depth-First Search and Breadth-First Search Algorithms

Explore the time complexities of Depth-First Search (DFS) and Breadth-First Search (BFS) algorithms. Understand how these graph traversal methods perform and their efficiency.
---
Disclaimer/Disclosure: Some of the content was synthetically produced using various Generative AI (artificial intelligence) tools; so, there may be inaccuracies or misleading information present in the video. Please consider this before relying on the content to make any decisions or take any actions etc. If you still have any concerns, please feel free to write them in a comment. Thank you.
---
Understanding the Time Complexity of Depth-First Search and Breadth-First Search Algorithms

When working with graph traversal algorithms, two of the most commonly discussed methods are Depth-First Search (DFS) and Breadth-First Search (BFS). These algorithms are pivotal in various applications such as network analysis, pathfinding in AI, and more. A crucial aspect of these algorithms is their time complexity, which helps us understand their efficiency and performance.

Depth-First Search (DFS)

Depth-First Search is an algorithm that starts at the root node (or an arbitrary node in the case of a graph) and explores as far as possible along each branch before backtracking.

Time Complexity of DFS

The time complexity of DFS is determined by the sum of the time required to visit each vertex and traverse each edge. Here's the pseudocode for DFS:

[[See Video to Reveal this Text or Code Snippet]]

For a graph G containing V vertices and E edges, the time complexity of DFS can be expressed as:

[[See Video to Reveal this Text or Code Snippet]]

V: Time to visit each vertex.

E: Time to traverse each edge.

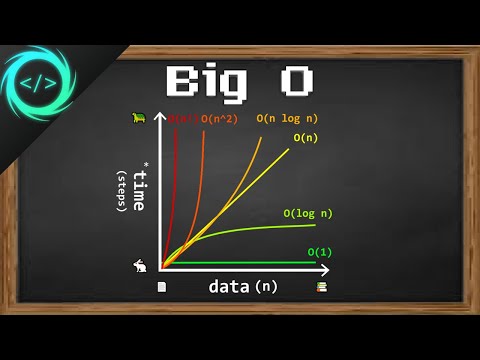
This complexity implies that DFS algorithm operates in linear time relative to the size of the graph, making it quite efficient for sparse graphs.

Breadth-First Search (BFS)

Breadth-First Search systematically explores the nodes level by level starting from the root node. It uses a queue to keep track of the next location to visit, ensuring it goes deeper into the graph uniformly.

Time Complexity of BFS

The time complexity of BFS is similarly influenced by the graph's vertices and edges. The following is a general pseudocode for BFS:

[[See Video to Reveal this Text or Code Snippet]]

For the graph G with V vertices and E edges, the time complexity of BFS is:

[[See Video to Reveal this Text or Code Snippet]]

Again, this means BFS also operates in linear time relative to the size of the graph. Like DFS, BFS has a balanced time efficiency but comes with its characteristic features suitable for different applications.

Conclusion

Both Depth-First Search (DFS) and Breadth-First Search (BFS) algorithms exhibit a time complexity of O(V + E), making them highly efficient for graph traversal tasks. While DFS is ideal for scenarios requiring exhaustive path exploration, BFS is optimal for finding the shortest path in unweighted graphs.

Understanding the context in which each of these algorithms operates best can significantly enhance their application in real-world problems.