filmov
tv
M.I.T. Integration Bee Question

Показать описание
University of Oxford mathematician Dr Tom Crawford solves a tricky integral from the MIT Integration Bee. The solution requires several changes of variables, completing the square and knowledge of hyperbolic functions.
The first step when solving the integral is to rewrite cosh in terms of exponentials. We then make the substitution u = exp(x) and complete the square in the denominator. A second change of variables for cosh(y) is then used to allow us to simplify the integrand using the hyperbolic identity cosh^(y) – sinh^2(y) = 1. Finally, we integrate cosech(y) and rewrite the resulting expression in terms of logs to get the desired result.
Check your working using the Maple Calculator App – available for free on Google Play and the App Store.
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
The first step when solving the integral is to rewrite cosh in terms of exponentials. We then make the substitution u = exp(x) and complete the square in the denominator. A second change of variables for cosh(y) is then used to allow us to simplify the integrand using the hyperbolic identity cosh^(y) – sinh^2(y) = 1. Finally, we integrate cosech(y) and rewrite the resulting expression in terms of logs to get the desired result.
Check your working using the Maple Calculator App – available for free on Google Play and the App Store.
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
Revisiting this integral from the MIT integration Bee
MIT is first to solve problem C
2023 MIT Integration Bee - Finals
How REAL Men Integrate Functions
An MIT Integration bee problem from @youngmathematician9154
MIT Integration Bee 2019 Problem 19 - The Hard/Long Way
THE IMPOSSIBLE MIT INTEGRATION BEE PROBLEM!!
Asking MIT students their major
MyDreamConnect Bootcamp (ADDITIONAL SUPPORT Events)
Speed Integrating HMMT 2019 Integration Bee Qualifying Exam
Moraine Valley Integration Bee
∫(cos(x) - xsin(x))/(x(x + cos(x)))dx . MIT Integration Bee 2010, Question 19, Qualifying Exam.
Columbia Integration Bee - 2022 finals - elimination round
MIT INTEGRATION BEE: INTEGRAL OF COS(X)COS(2X)...COS(6X) WITH A SNEAKY TRIG TRICK
2014 MIT Integration Bee Part 3/4
Gaussian Integral with a (Reciprocal) Twist: Berkeley Integration Bee (1)
MIT Integration Bee || Nope! I'm just wrong...spot my mistake in the comments!
Integration Bee Winners
MIT Integration Bee 15 -Concours de Calculs d'intégrales- sujet 2020-sin sin -x
Girls get caught eating candy in class on first day of school🍬🤣 #shorts
∫1/(1-x²) dx [-1/2,1/2]. MIT Integration Bee 2019, Question 4, Qualifying Exam. (Inverse Hyperbolic)...
MIT Intégration Bee 07- 2018 - Concours de Calculs d'intégrales- exp son et cos hyperbolique-7...
Integral of e^(3x) arctan e^(x) dx ; MIT Integration Bee Qualifying Exam 2015 : Question 14
∫1/(1 + sin(x)) dx. MIT Integration Bee 2018, Question 9, Qualifying Exam.
Комментарии
 0:11:58
0:11:58
 0:00:28
0:00:28
 0:28:09
0:28:09
 0:00:35
0:00:35
 0:36:41
0:36:41
 0:10:40
0:10:40
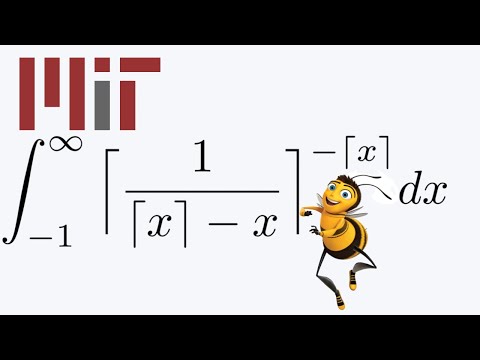 0:10:30
0:10:30
 0:00:27
0:00:27
 3:25:57
3:25:57
 0:20:13
0:20:13
 0:00:22
0:00:22
 0:01:00
0:01:00
 0:02:03
0:02:03
 0:01:00
0:01:00
 0:05:22
0:05:22
 0:10:22
0:10:22
 0:17:42
0:17:42
 0:01:35
0:01:35
 0:07:49
0:07:49
 0:00:39
0:00:39
![∫1/(1-x²) dx [-1/2,1/2].](https://i.ytimg.com/vi/-s2BXuCPBq4/hqdefault.jpg) 0:00:29
0:00:29
 0:02:34
0:02:34
 0:07:55
0:07:55
 0:00:37
0:00:37