Check whether a given point lies inside a triangle or not | GeeksforGeeks

Показать описание

This video is contributed by Harshit Verma

Please Like, Comment and Share the Video among your friends.

Also, Subscribe if you haven't already! :)

Рекомендации по теме

Комментарии

But how did you get the formula for area? I get that area of triangle is 1/2(base*ht) but how does the formula come by in case of any triangle

sbera

Since we are calculation area as float, the sum might not always be exactly equal to the bigger area and we may get wrong answer. We need to round off the areas.

rahulkhandelwal

If the area of the main triangle (points 1, 2, 3) is zero (and really a line segment) then this logic falls apart. The point tested could be on the line far away from the "triangle", but still on the line, and the areas would all add up to zero. If the main triangle has points that are co-located (and really a simple point), then the point tested can be anywhere at all and the function returns true. So watch out if "A" is zero...

gemhut

+ if A1 or A2 or A3 == 0 then the point is on the edge, any edge some like to consider as the point not inside the tringle if its on the edge

M.R.J-mmxv

Is there a way to do this with a quadrilateral (without splitting the quad into two tri's)

ned

Is there a possibility where the areas of the three triangles would be again equal to the area of the big one but the point would be outside ?

randomaccount

Clear and simple explanations (this is the definition of elegant ?). How about the general case of a triangle in 3D ?

YMO

it was glitchy so i had to do this

float D = abs(A - A1 - A2 - A3);

return D >= 0. && D < 0.001;

I have to do this in order for the triangle to look solid and not glitchy..

Kino-Imsureq

Excellent video, thank you for making it!

darrenwalsh

Just look to see if point P is on the same side of line AB as point C. Do the same for the other lines AC, BC, comparing with the opposite point. If they are all on the same side of the respective lines, then the point is in the triangle. It's very simple, very precise. If you deal with a vertical line, just compare the x coordinates. Your function that determines the side of a line that a point is on, should return either one side or the other, or on the line. You can return something like -1, 0 and 1 for this test. Don't make me post code.

gemhut

This is not very good way to do it because of precision issues

WowPlusWow

Check whether a given point lies inside a triangle or not | GeeksforGeeks

How to determine if a point lies on a line or not using the point and the equation

Check whether a given point lies inside a triangle or not | GeeksforGeeks

Checking if a point is inside a polygon is RIDICULOUSLY simple (Ray casting algorithm) - Inside code

Check if a point lies inside a triangle

Check if a point is inside a polygon | JavaScript code

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus

C Program To Check If Point Lies Inside, Outside or On The Circle

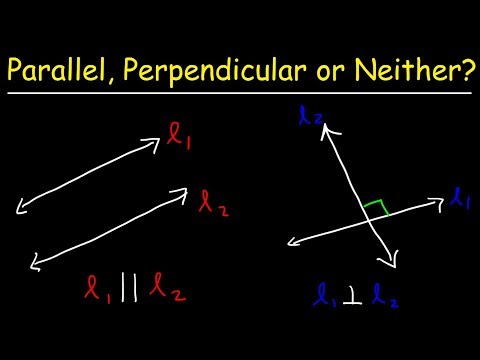
How To Tell If Two Lines Are Parallel, Perpendicular, or Neither?

Check if Point is Inside or Outside 2D Polygon (Patch Share)

How to Prove that a Point Lies on a Circle (or Inside/Outside)

OpenGL PP: Check whether a given point lies inside a triangle or not

How to check if two given line segments intersect? | GeeksforGeeks

Check Continuity of Function at Given Point

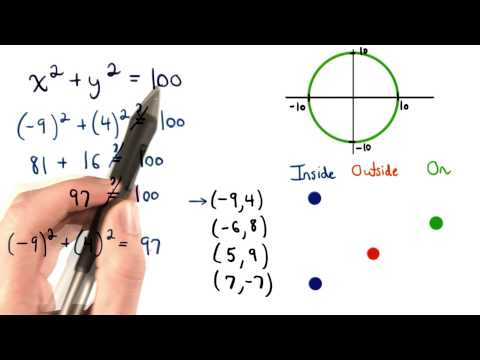
AQA Core 1 6.04 Determining whether a point lies Outside, On or Inside a Circle

Points Inside Outside On a Circle - Visualizing Algebra

Inflection point grade 12

How to Show that Three Points are Collinear or Not

Determine the discontinuity of the function

Determine if Lines are Parallel, Perpendicular or Neither

Check if Point is on the Line Ex 7

Determine whether the given point is a solution of the equation

Check if two line segments intersect

How To Find The Equation of a Plane Given Three Points

Continuity and Differentiability EXPLAINED with Examples