filmov
tv
How To Rationalize The Denominator Of a Surd

Показать описание
To rationalize the denominator means to eliminate any radical expressions in the denominator such as square roots and cube roots. The key idea is to multiply the original fraction by an appropriate value, such that after simplification, the denominator no longer contains radicals.
When the denominator is a monomial, the basic strategy is to apply the fact that
√x * √x = (√x)² = x
On the other hand, if the denominator is a binomial, the notion of conjugate comes in handy. The conjugate of a binomial is equal to the binomial itself, however, the middle sign is changed or switched.
And so if two conjugates are multiplied together, the result is always rational.
Example (√a+√b)(√a-√b) = √a²-√b² = a-b
and a-b is rational.
While dealing with Fractions in which the denominator is an irrational, to make it rational, you need to multiply the top and the bottom by the same irrational number on the denominator for a monomial surd.
For a binomial surd, you need to multiply the top and bottom by the conjugate of the denominator.
Join this channel to get access to perks:
When the denominator is a monomial, the basic strategy is to apply the fact that
√x * √x = (√x)² = x
On the other hand, if the denominator is a binomial, the notion of conjugate comes in handy. The conjugate of a binomial is equal to the binomial itself, however, the middle sign is changed or switched.
And so if two conjugates are multiplied together, the result is always rational.
Example (√a+√b)(√a-√b) = √a²-√b² = a-b
and a-b is rational.
While dealing with Fractions in which the denominator is an irrational, to make it rational, you need to multiply the top and the bottom by the same irrational number on the denominator for a monomial surd.
For a binomial surd, you need to multiply the top and bottom by the conjugate of the denominator.
Join this channel to get access to perks:
Комментарии
 0:05:28
0:05:28
 0:10:04
0:10:04
 0:10:18
0:10:18
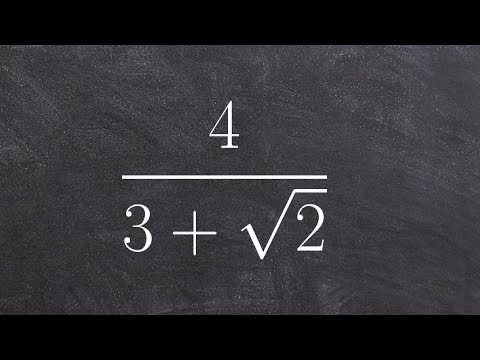 0:04:00
0:04:00
 0:10:55
0:10:55
 0:03:19
0:03:19
 0:02:39
0:02:39
 0:02:00
0:02:00
 0:10:50
0:10:50
 0:07:03
0:07:03
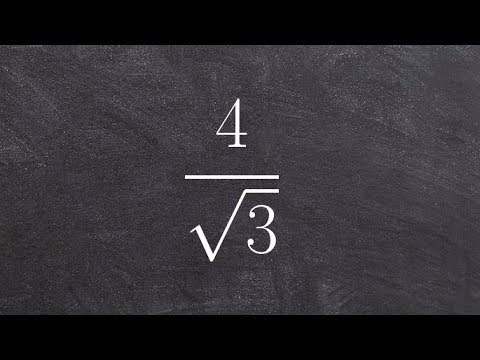 0:03:44
0:03:44
 0:14:32
0:14:32
 0:09:39
0:09:39
 0:00:29
0:00:29
 0:00:45
0:00:45
 0:03:06
0:03:06
 0:00:48
0:00:48
 0:05:13
0:05:13
 0:03:03
0:03:03
 0:05:48
0:05:48
 0:02:45
0:02:45
 0:07:44
0:07:44
 0:14:39
0:14:39
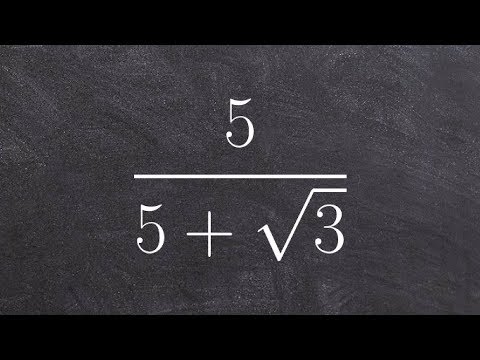 0:02:39
0:02:39