filmov
tv
JEE Advanced 2020 Paper 2- Limits Problem
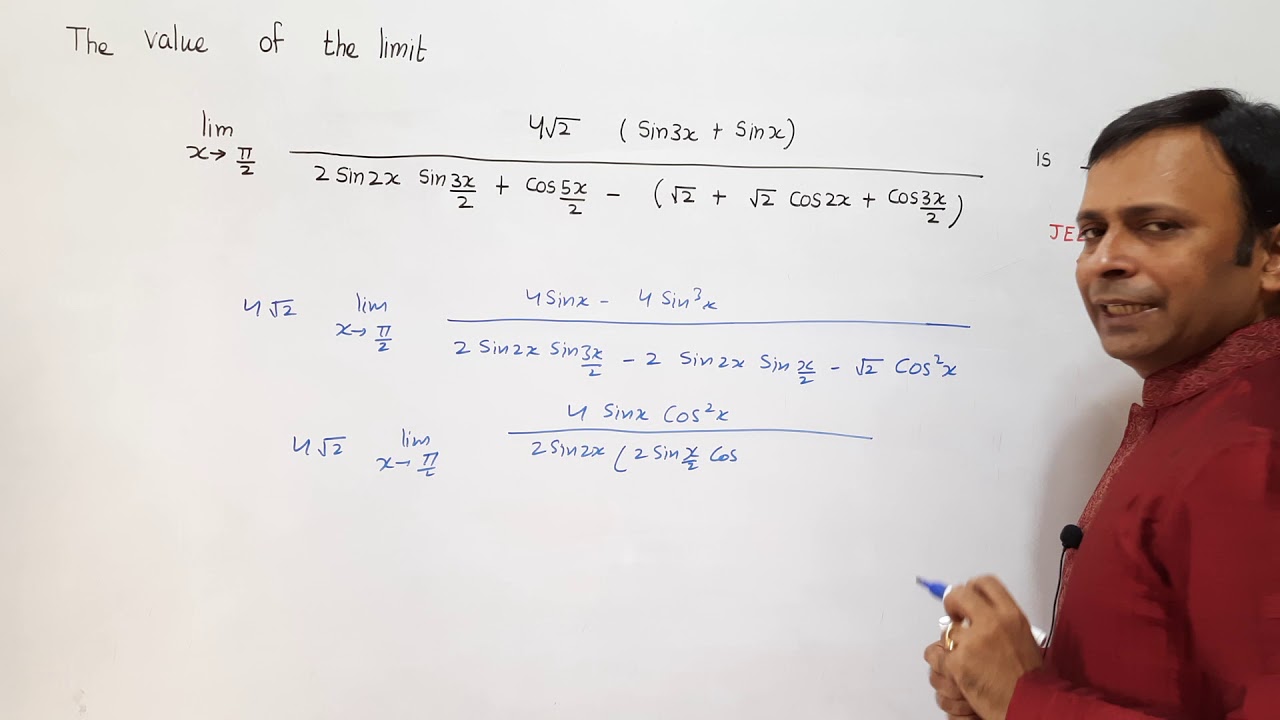
Показать описание
This video covers a highly challenging problem on Limits and gives a method to solve it in less than 2 minute with the help of graphs, which would otherwise take a very long time to solve. This is taken from recently held JEE Advanced 2020 Paper II question number 6 and the question is
The value of the limit limx→π/2 4√2(sin 3x + sin x)(2 sin 2x sin 3x/2 + cos5x/2) − (√2 + √2 cos 2x + cos3x/2) is _____
This video is suitable for the students aspiring for engineering entrance exam and is also suitable for CBSE, ISC, HSC, IB Board students and the students who have genuine interest in learning Calculus
#JEEAdvanced2020 #calculus #limits #challengingproblemonlimits #quicksolutiosofjeeadvanced #jeeadvancedcalculus #jeeadvanceddifferentialcalculus #jeeadvanced2020paper2solutions #IIT #iitjee #EDUCATION #CBSE #IITJEE #JEEMains #Mathematics #Science #kota #student #exam #student #maths #indian #jeeprepareation #engineering #kotacoaching #mathematics #iitbombay #iitmadras #iitkanpur #iitkharagpur #class #college #student #motivation #study #nta #upsc #iitcoaching #iitians #topper #iitmain #kotafactory #jeeaspirants #school #cet #exams #BITSAT #jeeadvancedpaper2Q5 #KVPY #JEEAdvanced2020paper2Q6
The value of the limit limx→π/2 4√2(sin 3x + sin x)(2 sin 2x sin 3x/2 + cos5x/2) − (√2 + √2 cos 2x + cos3x/2) is _____
This video is suitable for the students aspiring for engineering entrance exam and is also suitable for CBSE, ISC, HSC, IB Board students and the students who have genuine interest in learning Calculus
#JEEAdvanced2020 #calculus #limits #challengingproblemonlimits #quicksolutiosofjeeadvanced #jeeadvancedcalculus #jeeadvanceddifferentialcalculus #jeeadvanced2020paper2solutions #IIT #iitjee #EDUCATION #CBSE #IITJEE #JEEMains #Mathematics #Science #kota #student #exam #student #maths #indian #jeeprepareation #engineering #kotacoaching #mathematics #iitbombay #iitmadras #iitkanpur #iitkharagpur #class #college #student #motivation #study #nta #upsc #iitcoaching #iitians #topper #iitmain #kotafactory #jeeaspirants #school #cet #exams #BITSAT #jeeadvancedpaper2Q5 #KVPY #JEEAdvanced2020paper2Q6
JEE Advanced 2020 Physics Speed Solutions (Paper 2) | Q. 1 to 6
JEE Advanced 2020: Maths Paper - 2 Solution | Unacademy JEE | Nishant Vora
JEE Advanced 2020: Chemistry Paper - 2 Solution | Unacademy JEE | Anupam Gupta
JEE Advanced 2020 Physics Speed Solutions (Paper 2)| Q. 13 to 18
JEE Advanced 2020 Maths Solutions Paper 2
JEE Advanced 2020 | Video 1 | PHYSICS | Paper 2 Solutions - MCQ | NV Sir
Interesting Fact about JEE Advanced 2020 Paper !
IIT-JEE Advanced 2020 | Video Solutions | PHYSICS PAPER 2 | Vyas Edification
JEE Advanced 2020 SOLUTIONS PHYSICS PAPER 2 Q 4 to 6
JEE Advanced 2020 SOLUTIONS MATHEMATICS PAPER 2 Q 13 to 15
JEE Advanced 2020 SOLUTIONS CHEMISTRY PAPER 2 Q 10 to 12
JEE Advanced 2020 Physics Speed Solutions (Paper 2)| Q. 7 to 12
JEE Advanced 2020 SOLUTIONS MATHEMATICS PAPER 2 Q 16 to 18
JEE Advanced 2020 SOLUTIONS MATHEMATICS PAPER 2 Q 1 to 3
JEE Advanced 2020 SOLUTIONS CHEMISTRY PAPER 2 Q 01 to 03
JEE Advanced 2020 SOLUTIONS PHYSICS PAPER 2 Q 16 to 18
JEE Advanced 2020 Video Solutions Paper-2 Revised by AR Sir & AVN Sir | Physics| Motion Kota
JEE Advanced 2020 | Video 5 | PHYSICS Paper 2 Solutions - Multiple Correct Answer | NV Sir
JEE Advanced 2020 SOLUTIONS MATHEMATICS PAPER 2 Q 4 to 6
JEE Advanced 2020 | Video 2 | PHYSICS Paper 2 Solutions - MCQ | NV Sir
JEE Advanced 2020 Paper Solution | Maths Paper-2 | Manoj Sharma (MS) Sir | ETOOSINDIA
JEE Advanced 2020 Solutions | 🤔 Why BONUS ? | A learning for all IIT JEE Aspirants | Ray Optics
JEE Advanced 2020 Paper Solution | Physics (Paper - 2) | Muqeem Khan (MK Sir) | ETOOSINDIA
JEE Advanced 2020 SOLUTIONS PHYSICS PAPER 2 Q 1 to 3
Комментарии
 0:41:31
0:41:31
 2:06:54
2:06:54
 1:13:05
1:13:05
 0:31:05
0:31:05
 1:11:26
1:11:26
 0:26:15
0:26:15
 0:00:45
0:00:45
 1:46:36
1:46:36
 0:17:50
0:17:50
 0:10:54
0:10:54
 0:10:38
0:10:38
 0:25:26
0:25:26
 0:10:37
0:10:37
 0:12:12
0:12:12
 0:05:47
0:05:47
 0:08:02
0:08:02
 1:26:52
1:26:52
 0:21:14
0:21:14
 0:14:19
0:14:19
 0:16:38
0:16:38
 1:31:25
1:31:25
 0:09:38
0:09:38
 0:54:12
0:54:12
 0:14:49
0:14:49