filmov
tv
Linear Algebra Lecture 9.1 Normal Operators

Показать описание
00:00 Recap
00:20 Problems
02:37 Normal Operators
06:15 An Important Lemma
09:32 A Criterion for Normality
12:46 A Corollary
13:06 Normal Operators and Invariant Subspaces
Note: The auto-generated subtitles are mostly accurate and may enhance experience.
Prerequisites: Familiarity with mathematical notation and terminology.
----------
Thanks to my Patreon Supporters:
Namrata Khetan
Hersh
----------
#LinearAlgebra
#CSIRNET
#GATE
00:20 Problems
02:37 Normal Operators
06:15 An Important Lemma
09:32 A Criterion for Normality
12:46 A Corollary
13:06 Normal Operators and Invariant Subspaces
Note: The auto-generated subtitles are mostly accurate and may enhance experience.
Prerequisites: Familiarity with mathematical notation and terminology.
----------
Thanks to my Patreon Supporters:
Namrata Khetan
Hersh
----------
#LinearAlgebra
#CSIRNET
#GATE
Linear Algebra - Lecture 9 - Matrix Equations
Linear Algebra Lecture 9 | Using Elementary Matrices to find the Inverse of a Matrix
Linear Algebra - Lecture 9: The Mechanics of Matrix Multiplication
Lecture 9: Numerical Linear Algebra Primer
Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers
Linear Algebra II (G30 Program): Lecture 9: Spectral theorem
Linear Algebra 99, Normal Matrices
Dot products and duality | Chapter 9, Essence of linear algebra
Determinant of a Matrix Class 9
How REAL Men Integrate Functions
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
Gauss Jordan Elimination & Reduced Row Echelon Form
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Row Echelon Form of the Matrix Explained | Linear Algebra
HOWARD ANTON LINEAR ALGEBRA LECTURE 9
How to find Inverse of a Matrix Using Calculator #youtubeshorts #shortsviral #viral
How to Find the Matrix of a Linear Transformation
Vectors | Chapter 1, Essence of linear algebra
How to Find the Rank of a Matrix (with echelon form) | Linear Algebra
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Venn diagram in set theory. #settheory
Lecture-9 Matrix Algebra-Solution of Simultaneous Linear System in Hindi
How to find determinant of 3x3 Matrix Using calculator #viral #calculatortricks #youtubeshorts
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Комментарии
 0:18:49
0:18:49
 0:34:24
0:34:24
 0:33:14
0:33:14
 1:19:10
1:19:10
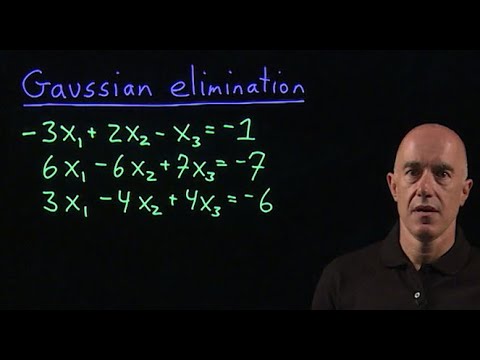 0:14:00
0:14:00
 1:03:09
1:03:09
 0:04:26
0:04:26
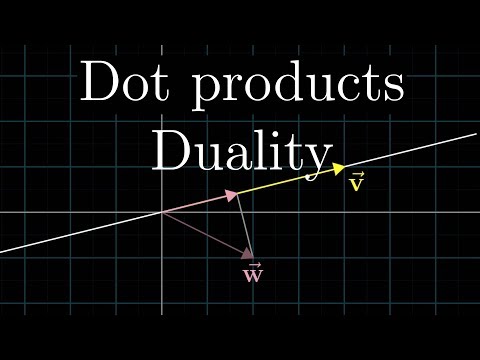 0:14:12
0:14:12
 0:00:18
0:00:18
 0:00:35
0:00:35
 0:00:20
0:00:20
 0:10:51
0:10:51
 0:00:16
0:00:16
 0:11:11
0:11:11
 0:57:41
0:57:41
 0:00:50
0:00:50
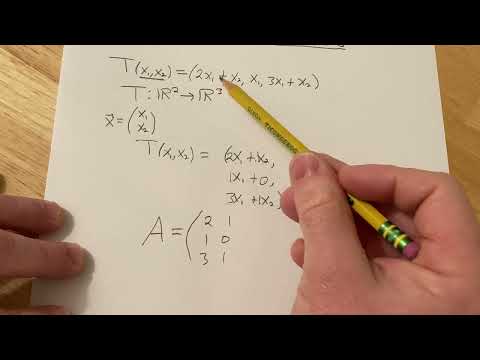 0:05:19
0:05:19
 0:09:52
0:09:52
 0:03:25
0:03:25
 0:10:59
0:10:59
 0:00:30
0:00:30
 0:19:07
0:19:07
 0:01:00
0:01:00
 0:00:15
0:00:15