filmov
tv
Solving Linear Programming Problems: Introducing the Simplex Method Example 1
Показать описание
Simplex Method for Linear Programming Problem.
Welcome to our comprehensive video tutorial on solving linear programming problems using the Simplex Method. In this video, we will guide you through the step-by-step process of applying the Simplex Method to optimize linear programming models and find optimal solutions.
Linear programming is a powerful mathematical technique used to maximize or minimize a linear objective function subject to a set of linear constraints. The Simplex Method is a widely employed algorithm that systematically searches for the optimal solution within the feasible region.
We begin by introducing the basics of linear programming, including the objective function, decision variables, and linear constraints. We explain the concept of the feasible region, which represents the set of all valid solutions satisfying the constraints. Our goal is to find the optimal solution that maximizes or minimizes the objective function within this region.
Next, we delve into the Simplex Method, a systematic approach to iteratively improve the solution until the optimal point is reached. We discuss the fundamental components of the Simplex Method, such as the simplex tableau, pivot operations, and the concept of optimality. We explain how the method identifies the next pivot element, updates the tableau, and proceeds to the next iteration.
Throughout the video, we provide clear explanations, visual representations of the simplex tableau, and practical examples to illustrate the steps involved in the Simplex Method. We demonstrate how to set up the initial tableau, perform pivot operations, and interpret the results at each iteration.
We also discuss important concepts such as degeneracy, unboundedness, and infeasibility, and explain how to handle these scenarios within the Simplex Method framework. We provide insights on strategies to avoid cycling, a situation where the Simplex Method gets stuck in a loop without making progress.
By the end of this video, you will have a solid understanding of the Simplex Method and its application to linear programming problems. You will be equipped with the skills to set up and solve linear programming models, analyze the results from the simplex tableau, and interpret the optimal solution within the context of the problem.
Whether you are a student studying optimization techniques, a business professional involved in decision-making processes, or someone interested in the applications of linear programming, this video is a valuable resource. Join us as we demystify the Simplex Method and empower you to solve complex linear programming problems.
Prepare to enhance your problem-solving abilities, deepen your understanding of linear programming, and master the art of finding optimal solutions with the Simplex Method. Let's embark on this captivating journey into the world of linear programming optimization!
Graphical method
Optimization Techniques
Welcome to our comprehensive video tutorial on solving linear programming problems using the Simplex Method. In this video, we will guide you through the step-by-step process of applying the Simplex Method to optimize linear programming models and find optimal solutions.
Linear programming is a powerful mathematical technique used to maximize or minimize a linear objective function subject to a set of linear constraints. The Simplex Method is a widely employed algorithm that systematically searches for the optimal solution within the feasible region.
We begin by introducing the basics of linear programming, including the objective function, decision variables, and linear constraints. We explain the concept of the feasible region, which represents the set of all valid solutions satisfying the constraints. Our goal is to find the optimal solution that maximizes or minimizes the objective function within this region.
Next, we delve into the Simplex Method, a systematic approach to iteratively improve the solution until the optimal point is reached. We discuss the fundamental components of the Simplex Method, such as the simplex tableau, pivot operations, and the concept of optimality. We explain how the method identifies the next pivot element, updates the tableau, and proceeds to the next iteration.
Throughout the video, we provide clear explanations, visual representations of the simplex tableau, and practical examples to illustrate the steps involved in the Simplex Method. We demonstrate how to set up the initial tableau, perform pivot operations, and interpret the results at each iteration.
We also discuss important concepts such as degeneracy, unboundedness, and infeasibility, and explain how to handle these scenarios within the Simplex Method framework. We provide insights on strategies to avoid cycling, a situation where the Simplex Method gets stuck in a loop without making progress.
By the end of this video, you will have a solid understanding of the Simplex Method and its application to linear programming problems. You will be equipped with the skills to set up and solve linear programming models, analyze the results from the simplex tableau, and interpret the optimal solution within the context of the problem.
Whether you are a student studying optimization techniques, a business professional involved in decision-making processes, or someone interested in the applications of linear programming, this video is a valuable resource. Join us as we demystify the Simplex Method and empower you to solve complex linear programming problems.
Prepare to enhance your problem-solving abilities, deepen your understanding of linear programming, and master the art of finding optimal solutions with the Simplex Method. Let's embark on this captivating journey into the world of linear programming optimization!
Graphical method
Optimization Techniques
0:33:20
0:14:23
0:18:56
0:15:08
0:03:49
0:12:40
0:18:03
0:05:44
0:03:59
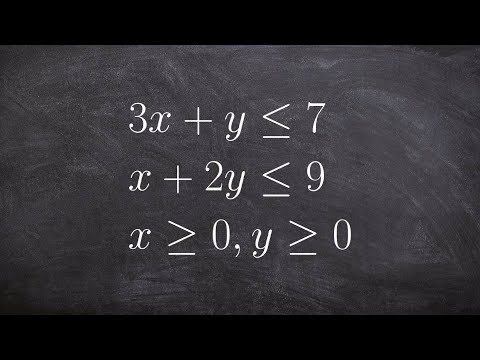0:06:43
0:05:22
0:15:34
0:05:43
0:41:05
0:00:05
0:15:09
0:10:42
0:30:44
0:07:16
0:25:22
0:41:24
0:05:31
1:14:55
0:26:31