filmov
tv
[Deprecated] Real Analysis Lecture 6.2 Continuity: Epsilon-Delta Definition
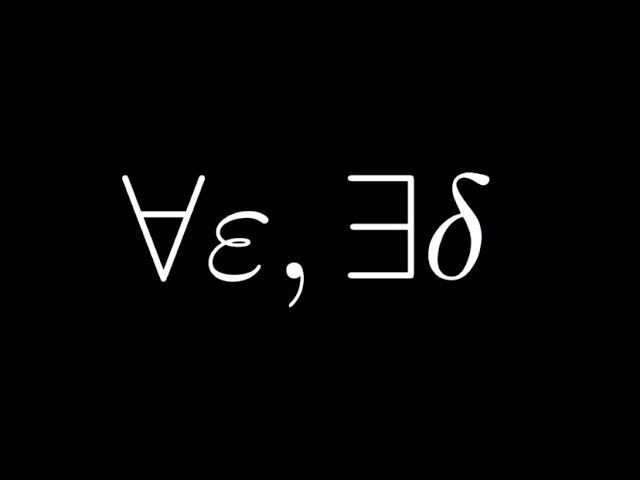
Показать описание
00:00 Recap
02:10 The Epsilon-Delta Definition
09:38 Continuity is a Local Property
Suggestion: Play at 1.25 times the normal speed.
Note: The auto-generated subtitles are mostly accurate and may enhance experience.
#RealAnalysis
02:10 The Epsilon-Delta Definition
09:38 Continuity is a Local Property
Suggestion: Play at 1.25 times the normal speed.
Note: The auto-generated subtitles are mostly accurate and may enhance experience.
#RealAnalysis
[Deprecated] Real Analysis Lecture 13.6 Product of Two Series
[Deprecated] Real Analysis Lecture 12.5 The Square Root of 2
[Deprecated] Real Analysis Lecture 6.1 Continuity: Geometric Definition
[Deprecated] Real Analysis Lecture 8.2 Limits and Monotone Functions
[DEPRECATED] Real Analysis Lecture 7.1 Intermediate Value Theorem
[Deprecated] Real Analysis Lecture 13.4 Positive Term Series
[Deprecated] Real Analysis Lecture 13.5 Absolute Convergence
[Deprecated] Real Analysis Lecture 4.6 Limit Inferior and Superior
[Deprecated] Real Analysis Lecture 9.3 Analytical Definition of Derivative
[Deprecated] The Pigeonhole Principle
[Deprecated] Real Analysis Lecture 10.1 Local and Global Extrema
Probability and Measure, Lecture 6: Integration and Convergence Theorems
DEPRECIATION OF NON CURRENT ASSETS (PART 2)
[Deprecated] Group Theory Lecture 0.7 Fundamental Theorem of Arithmetic
[Deprecated] A Brigade of 7 People
Elon Musk’s Incredible Speech on the Education System | Eye Opening Video on Education
Real Analysis Proofs - Exponential Function is Continuous
[Deprecated] Group Theory Lecture 0.6 Relatively Prime Integers
[Deprecated] Well Ordering Principle Lecture 1: The Statement and an Example
Depreciation and Disposal of Fixed Assets
Lecture 26.2 - Integration by Parts
Countability of the Rational Numbers - Real Analysis | Lecture 9
Real Analysis, Lecture 16 (The Exponential function)
Deprecation Expense
Комментарии
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/dNS6yKARMoY/hqdefault.jpg) 0:20:49
0:20:49
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/kxT6_3Wg5xQ/hqdefault.jpg) 0:12:56
0:12:56
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/elvlTbhEm7w/hqdefault.jpg) 0:34:50
0:34:50
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/MlVqcV8i3-I/hqdefault.jpg) 0:16:46
0:16:46
![[DEPRECATED] Real Analysis](https://i.ytimg.com/vi/HOdEfkQLDpQ/hqdefault.jpg) 0:24:29
0:24:29
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/nRIbuGb_yEc/hqdefault.jpg) 0:17:00
0:17:00
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/PKQ1Vx9TKVg/hqdefault.jpg) 0:21:49
0:21:49
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/eumxDsm7264/hqdefault.jpg) 0:17:49
0:17:49
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/Y-VqqE_L_2Y/hqdefault.jpg) 0:28:04
0:28:04
![[Deprecated] The Pigeonhole](https://i.ytimg.com/vi/gZpfWgr584U/hqdefault.jpg) 0:20:51
0:20:51
![[Deprecated] Real Analysis](https://i.ytimg.com/vi/S_DJCdpdZFo/hqdefault.jpg) 0:16:11
0:16:11
 1:58:19
1:58:19
 1:00:10
1:00:10
![[Deprecated] Group Theory](https://i.ytimg.com/vi/wGBJRNKCQCo/hqdefault.jpg) 0:17:32
0:17:32
![[Deprecated] A Brigade](https://i.ytimg.com/vi/XtBRXif-UVM/hqdefault.jpg) 0:09:04
0:09:04
 0:10:56
0:10:56
 0:05:04
0:05:04
![[Deprecated] Group Theory](https://i.ytimg.com/vi/T7NwoVJtn1I/hqdefault.jpg) 0:08:26
0:08:26
![[Deprecated] Well Ordering](https://i.ytimg.com/vi/XVQAIXyhfH8/hqdefault.jpg) 0:14:24
0:14:24
 0:07:18
0:07:18
 0:06:17
0:06:17
 0:52:04
0:52:04
 0:51:57
0:51:57
 0:26:13
0:26:13