filmov
tv
Write the equation of an ellipse given the center, vertex and focus

Показать описание
Learn how to write the equation of an ellipse from its properties. The equation of an ellipse comprises of three major properties of the ellipse: the major radius (a), the minor radius (b) and the center (h, k). The ellipse is vertical if the major radius in vertical and the ellipse is horizontal if the major radius is horizontal.
When given the two foci of the ellipse, the center of the ellipse is halfway between the two foci. When given the vertices of an ellipse, the major radius of an ellipse is the distance between the center of the ellipse and its vertices. Using the pythagoras identity for the relationship between the focal length (distance between the center and the foci) and the radius, we can obtain the minor radius.
After obtaining the center, the major and the minor radius, they are plugged into the equation of an ellipse to obtain the desired equation.
Follow us on
#conicsections #ellipseconicsections
When given the two foci of the ellipse, the center of the ellipse is halfway between the two foci. When given the vertices of an ellipse, the major radius of an ellipse is the distance between the center of the ellipse and its vertices. Using the pythagoras identity for the relationship between the focal length (distance between the center and the foci) and the radius, we can obtain the minor radius.
After obtaining the center, the major and the minor radius, they are plugged into the equation of an ellipse to obtain the desired equation.
Follow us on
#conicsections #ellipseconicsections
Math Help : How to Write an Equation
How To Find The Equation of a Line From a Graph | Algebra
Writing the equation from a graph
Writing the equation of a line given two points
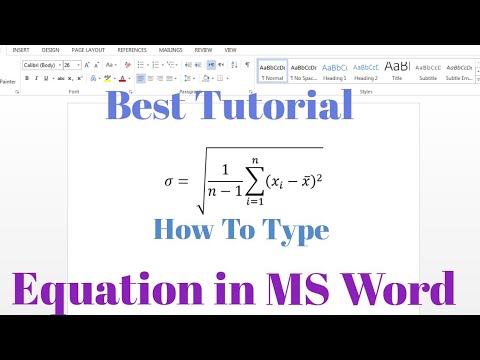
How to write an equation or formula in Word.
How To Write The Equation of a Line Given The Slope and a Point | Algebra
How To Write a Linear Equation From a Function Table | Algebra
How To Type Equation In Microsoft Word | Writing Equation In Word | Best Tutorial
Write an equation that is perpendicular to the given equation
Write the equation of a line given a slope and a point the line runs through
Linear Equations - Algebra
write an equation of a parabola from a given graph
Writing the Equation of a Line Given the Y-Intercept and Another Point
How To Write The Equation of a Line Given The X and Y Intercepts | Algebra
How To Find The Equation of a Quadratic Function From a Graph
How to write an equation from standard form to slope intercept form
How to write a linear equation in standard form
Writing an equation using point slope form given a point and slope
Write Algebraic Equation for the Statements
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
Writing an equation given the slope and y intercept
Write the equation of an ellipse given the foci and vertices
Writing an equation using point slope form given two points
Writing A Linear Equation From A Function Table
Комментарии
 0:02:40
0:02:40
 0:10:05
0:10:05
 0:02:09
0:02:09
 0:03:25
0:03:25
 0:03:38
0:03:38
 0:08:32
0:08:32
 0:14:51
0:14:51
 0:04:07
0:04:07
 0:03:09
0:03:09
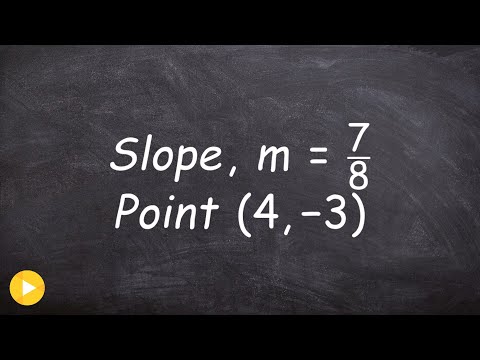 0:04:37
0:04:37
 0:32:05
0:32:05
 0:06:49
0:06:49
 0:00:58
0:00:58
 0:05:07
0:05:07
 0:09:35
0:09:35
 0:03:06
0:03:06
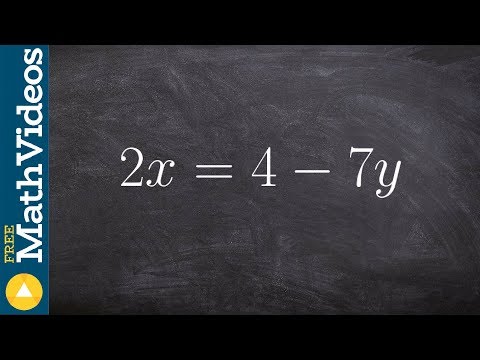 0:02:19
0:02:19
 0:02:03
0:02:03
 0:03:44
0:03:44
 0:06:54
0:06:54
 0:01:03
0:01:03
 0:05:52
0:05:52
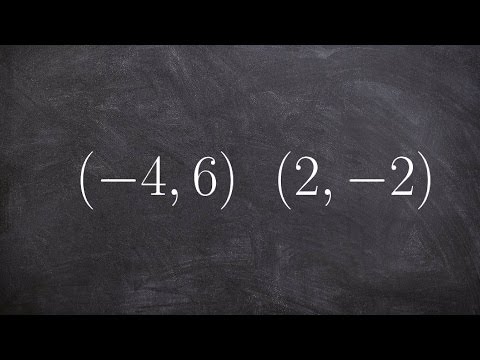 0:03:43
0:03:43
 0:08:40
0:08:40