filmov
tv
MATRICES AND DETERMINANTS | ONE SHOT SUPER REVISION | JEE MAINS AND ADVANCED | Q6
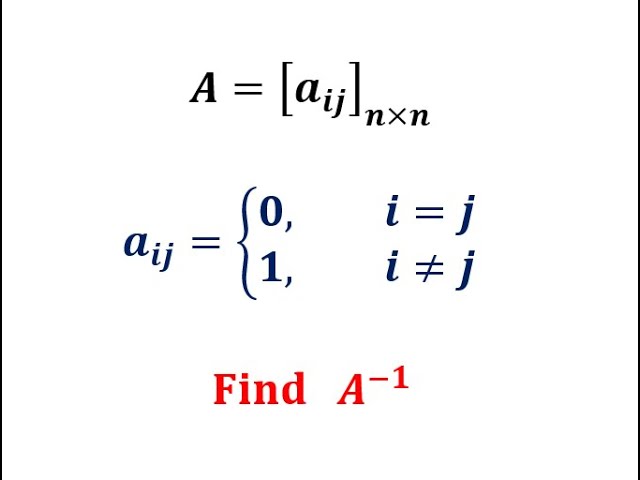
Показать описание
jee mains 2022 and jee advanced 2022 matrices and determinants aspirants helpful most important problems
MATRICES AND DETERMINANTS | ONE SHOT SUPER REVISION | JEE MAINS AND ADVANCED
class 12 matrices and determinants cbse boards iit jee
1. matrices and determinants iit jee
2. matrices and determinants class 11 iit jee
3. matrices and determinants jee
4. jee main mathematics matrices and determinants
5. iit matrices and determinants
6. iit matrices and determinants questions
7. matrices and determinants iit jee questions
8. matrices and determinants jee questions
9. jee matrices and determinants questions
10. matrices and determinants class 11 jee questions
11. matrices and determinants previous year questions jee
12. matrices and determinants iit jee
13. matrices and determinants iit jee questions with solutions
14. matrices and determinants iit jee revision
15. matrices and determinants iit jee previous year question
matrices and determinants Q6. A is a matrix such that aij = 0, i=j and 1, i not equal to j. Find inverse of A.
#online_coaching
#online_free_coaching
#StayHomeAndLearn #JEEMainMaths
#JEEAdvanceMaths
#matrices
#determinants
#matrices_and_determinants
#IITJEE
#JEE
MATRICES AND DETERMINANTS | ONE SHOT SUPER REVISION | JEE MAINS AND ADVANCED
class 12 matrices and determinants cbse boards iit jee
1. matrices and determinants iit jee
2. matrices and determinants class 11 iit jee
3. matrices and determinants jee
4. jee main mathematics matrices and determinants
5. iit matrices and determinants
6. iit matrices and determinants questions
7. matrices and determinants iit jee questions
8. matrices and determinants jee questions
9. jee matrices and determinants questions
10. matrices and determinants class 11 jee questions
11. matrices and determinants previous year questions jee
12. matrices and determinants iit jee
13. matrices and determinants iit jee questions with solutions
14. matrices and determinants iit jee revision
15. matrices and determinants iit jee previous year question
matrices and determinants Q6. A is a matrix such that aij = 0, i=j and 1, i not equal to j. Find inverse of A.
#online_coaching
#online_free_coaching
#StayHomeAndLearn #JEEMainMaths
#JEEAdvanceMaths
#matrices
#determinants
#matrices_and_determinants
#IITJEE
#JEE
Комментарии
 2:41:55
2:41:55
 0:10:03
0:10:03
 0:10:17
0:10:17
 1:29:25
1:29:25
 1:27:16
1:27:16
 0:29:31
0:29:31
 2:23:56
2:23:56
 0:30:29
0:30:29
 0:33:40
0:33:40
 1:33:31
1:33:31
 0:05:31
0:05:31
 2:11:31
2:11:31
 0:00:18
0:00:18
 0:01:33
0:01:33
 2:24:17
2:24:17
 0:00:33
0:00:33
 1:36:51
1:36:51
 0:10:59
0:10:59
 8:11:02
8:11:02
 0:01:13
0:01:13
 0:11:23
0:11:23
 0:07:08
0:07:08
 3:31:43
3:31:43
 3:37:34
3:37:34