filmov
tv
Statement I (Assertion) and Statement 11 (Reason) Each of these que...

Показать описание
Statement I (Assertion) and Statement 11 (Reason)
Each of these questions also has four alternatives choices, only one of which is the correct answer. You have to select the correct choice, as given below.
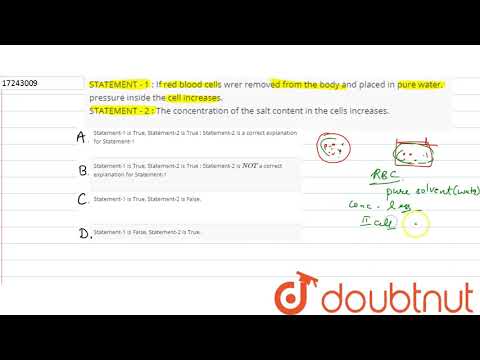
(a) Statement \( I \) is true, Statement \( I I \) is true and Statement \( I \) is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true but Statement II is not a correct explanation for Statement \( I \).
(c) Statement \( I \) is true, Statement \( I I \) is false.
(d) Statement \( \mathrm{I} \) is false, Statement \( \mathrm{I} \) is true.
Statement I Let \( \mathbf{a}, \mathbf{b}, \mathbf{c} \) and \( \mathrm{d} \) are position vector four points \( A, B, C \) and \( D \) and \( 3 a-2 b+5 c-6 d=0 \), then points \( A, B, C \) and \( D \) are coplanar.
Statement II Three non-zero, linearly dependent coinitial vectors (PQ. PR and \( \mathbf{P S}) \) are coplanar.
Each of these questions also has four alternatives choices, only one of which is the correct answer. You have to select the correct choice, as given below.
(a) Statement \( I \) is true, Statement \( I I \) is true and Statement \( I \) is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true but Statement II is not a correct explanation for Statement \( I \).
(c) Statement \( I \) is true, Statement \( I I \) is false.
(d) Statement \( \mathrm{I} \) is false, Statement \( \mathrm{I} \) is true.
Statement I Let \( \mathbf{a}, \mathbf{b}, \mathbf{c} \) and \( \mathrm{d} \) are position vector four points \( A, B, C \) and \( D \) and \( 3 a-2 b+5 c-6 d=0 \), then points \( A, B, C \) and \( D \) are coplanar.
Statement II Three non-zero, linearly dependent coinitial vectors (PQ. PR and \( \mathbf{P S}) \) are coplanar.
 0:04:57
0:04:57
 0:02:53
0:02:53
 0:02:19
0:02:19
 0:06:36
0:06:36
 0:01:25
0:01:25
 0:11:43
0:11:43
 0:06:28
0:06:28
 0:02:00
0:02:00
 0:02:28
0:02:28
 0:01:53
0:01:53
 0:02:03
0:02:03
 0:02:04
0:02:04
 0:01:50
0:01:50
 0:03:30
0:03:30
 0:02:18
0:02:18
 0:02:18
0:02:18
 0:01:18
0:01:18
 0:02:04
0:02:04
 0:07:37
0:07:37
 0:14:15
0:14:15
 0:15:28
0:15:28
 0:08:25
0:08:25
 0:01:35
0:01:35
 0:01:28
0:01:28