Algebra 1 Practice - Graph an Equation Using Slope-Intercept Form (Example 3)

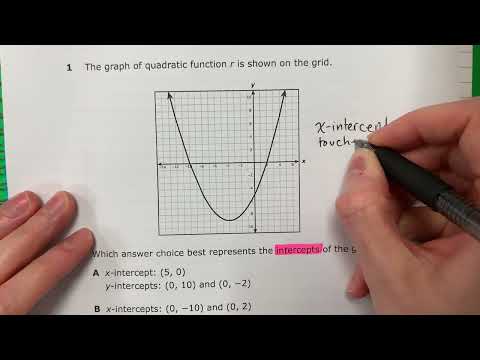
Graphing an equation using the slope-intercept form is a straightforward process once you understand how the slope and y-intercept work. The slope-intercept form of a linear equation is:

\[
y = mx + b
\]

Where:
- \(m\) is the slope of the line.
- \(b\) is the y-intercept, the point where the line crosses the y-axis.

### Steps to Graph an Equation Using Slope-Intercept Form

#### Step 1: Identify the Slope and Y-Intercept
- **Y-Intercept \(b\)**: This is the starting point on the graph. It tells you where the line crosses the y-axis (where \(x = 0\)).
- **Slope \(m\)**: This tells you how steep the line is and in which direction it moves. The slope is often expressed as a fraction \(\frac{\text{rise}}{\text{run}}\), indicating how much the line moves up or down for every unit it moves horizontally.

#### Step 2: Plot the Y-Intercept
- Start by finding the y-intercept on the graph.
- Plot a point at \((0, b)\) on the y-axis.

**Example**: If your equation is \(y = 2x + 3\), the y-intercept \(b\) is 3. So, you would plot a point at \((0, 3)\) on the graph.

#### Step 3: Use the Slope to Find Another Point
- From the y-intercept, use the slope to determine the next point on the line.
- If the slope \(m\) is positive, move up and to the right.
- If the slope \(m\) is negative, move down and to the right.
- The slope is a ratio \(\frac{\text{rise}}{\text{run}}\):
- **Rise**: Move vertically (up if positive, down if negative).
- **Run**: Move horizontally (always to the right).

**Example**: For the equation \(y = 2x + 3\), the slope \(m = 2\) can be written as \(\frac{2}{1}\), meaning from \((0, 3)\), move up 2 units (rise) and 1 unit to the right (run) to get the point \((1, 5)\).

#### Step 4: Plot the Second Point
- Plot the second point using the rise and run from the y-intercept.
- In the example, plot the point \((1, 5)\).

#### Step 5: Draw the Line
- Connect the two points with a straight line.
- Extend the line across the graph, and add arrows at both ends to indicate that it continues indefinitely.

#### Step 6: Check Additional Points (Optional)
- To ensure accuracy, you can choose another value of \(x\), substitute it into the equation, and plot the resulting point.
- Draw the line to confirm it passes through all the plotted points.

### Example: Graphing \(y = -\frac{1}{2}x + 4\)

1. **Identify the y-intercept**: \(b = 4\). Plot the point \((0, 4)\).
2. **Identify the slope**: \(m = -\frac{1}{2}\). From \((0, 4)\), move down 1 unit (rise) and 2 units to the right (run) to get the point \((2, 3)\).
3. **Plot the second point**: Place a point at \((2, 3)\).
4. **Draw the line**: Connect the points with a straight line.

By following these steps, you can graph any linear equation given in slope-intercept form. This method is useful for quickly and accurately visualizing the relationship between \(x\) and \(y\).

I have many informative videos for Pre-Algebra, Algebra 1, Algebra 2, Geometry, Pre-Calculus, and Calculus. Please check it out:

/ nickperich

Nick Perich
Norristown Area High School
Norristown Area School District
Norristown, Pa

#math #algebra #algebra2 #maths