filmov
tv
Solve the System of Equations with Variables: ax - by = 0 and ay - bx = (a^2 - b^2)/(ab)

Показать описание
Solve the System of Equations with Variables: ax - by = 0 and ay - bx = (a^2 - b^2)/(ab)
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
How do we solve a system of linear equations using any method
Solving Systems of Equations By Elimination & Substitution With 2 Variables
Solving Systems of Equations With 3 Variables & Word Problems
Learn to solve a system of equations using substitution
Solving Systems of Equations By Graphing
Substitution Method to Solve a System of Equations
Solving systems of equations by elimination | Algebra Basics | Khan Academy
Solving Systems of Equations... Elimination Method (NancyPi)
Think You Can Solve This Math Problem? Olympiad Style! #Trigonometry
Solving Systems of Linear Equations By Graphing │Algebra
One Solution, No Solution, or Infinitely Many Solutions - Consistent & Inconsistent Systems
Solve a system of three variables
Solve a system of linear equations using substitution
Solving Systems of Equations... Substitution Method (NancyPi)
What is the solution to the system of equations
Linear Algebra - 27 - Algebraic Systems of Equations with Matrices
Solving a system of equations by substitution
Solving a System of Equations Using Elimination and Multipliers
Elimination Method For Solving Systems of Linear Equations Using Addition and Multiplication, Algebr
SOLVING SYSTEMS OF EQUATIONS STEP-BY-STEP!
Substitution Method - Solving Systems of Linear Equations by │Algebra
Gaussian Elimination & Row Echelon Form
Elimination Method - Solving Systems of Equations │Algebra
Solving System of Linear Equations by Substitution Method | Solution of System of Equations
Комментарии
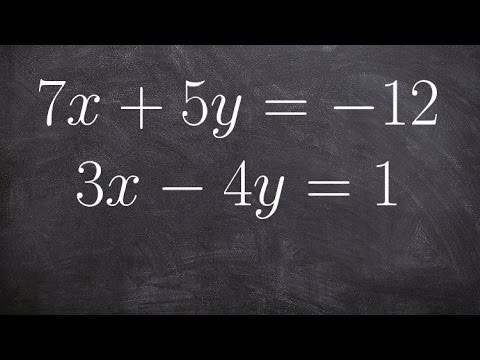 0:04:34
0:04:34
 0:10:27
0:10:27
 0:12:44
0:12:44
 0:05:17
0:05:17
 0:05:15
0:05:15
 0:03:47
0:03:47
 0:12:44
0:12:44
 0:19:44
0:19:44
 0:04:27
0:04:27
 0:10:52
0:10:52
 0:07:30
0:07:30
 0:12:45
0:12:45
 0:05:03
0:05:03
 0:18:30
0:18:30
 0:05:16
0:05:16
 0:07:18
0:07:18
 0:02:54
0:02:54
 0:03:48
0:03:48
 0:10:21
0:10:21
 0:04:49
0:04:49
 0:12:16
0:12:16
 0:18:40
0:18:40
 0:15:55
0:15:55
 0:12:28
0:12:28