filmov
tv
X = ?, Y = ?, Z = ? Solve This System of Equations | Step-by-Step Tutorial
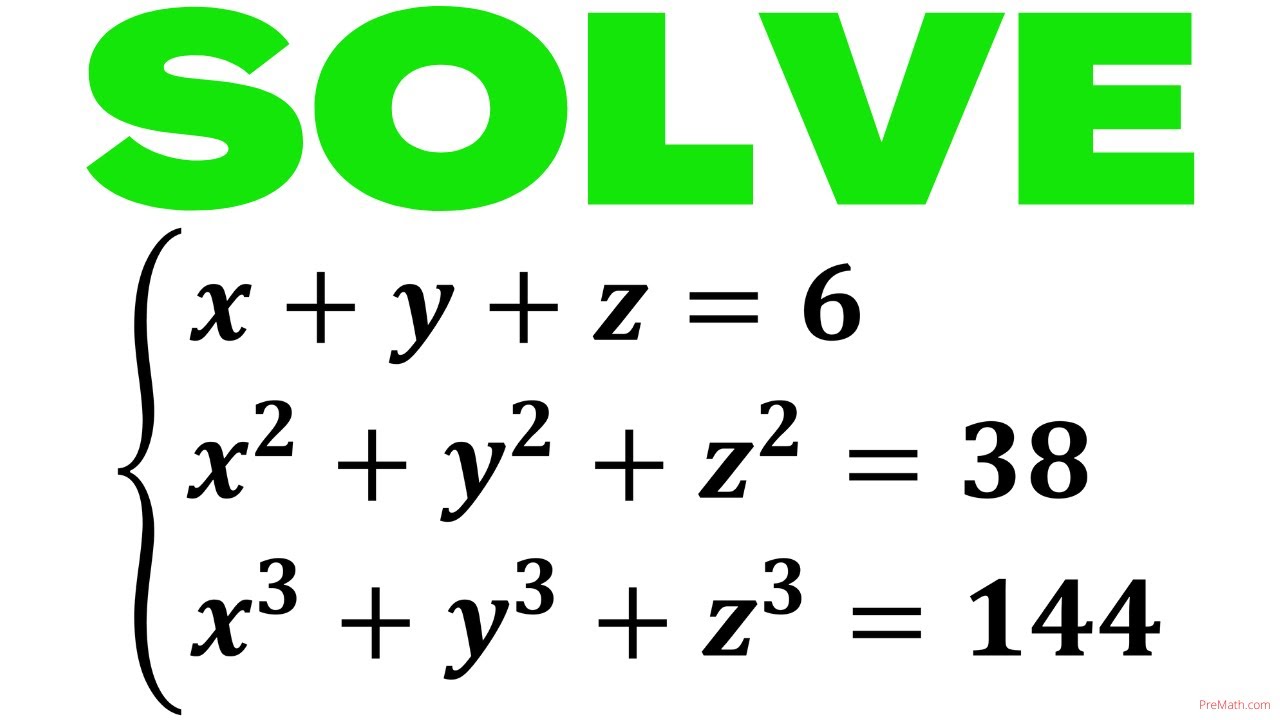
Показать описание
X + Y - Official UK Trailer
A Brilliant Young Mind (x+y) Nathan solving the Math Problem.
JELENA KARLEUŠA - XY - OMEGA
X+Y - Clip #2 Coin Toss
VITAA & SLIMANE - XY (Clip Officiel)
X & Y
Caity Baser - X&Y (Official Lyric Video)
X+Y Trailer | Festival 2014
A Brilliant Young Mind (X+Y) Piano & Synesthesia Scene - Bach/Gounod Ave Maria
X+Y - Clip #1 Mr Humphreys
Pokémon X and Y Are a Bit of a Contradiction
X+Y (soundtrack) Keaton Henson - Elevator song
XY / YG (Official Video)
X+Y - Clip #6 Flight
XY / GET STUPID (Official Video)
X&Y | Teaser2 'Kiss' | Romance w/ Ina Raymundo & Will Ashley
W/X/Y - Tani Yuuki (Official Lyric Video)
Do you understand this viral very good math movie clip? (Nathan solves math problem X+Y)
Will Ashley at Ina Raymundo, kinabahan sa intimate scene nila sa pelikulang 'X & Y' | ...
X+Y: Final Scene (Subtitulado)
I have a lot of feelings about pokemon X and Y
X-Axis and Y-Axis | The Coordinate Plane | What are the X and Y-Axes? | Math with Mr. J
Pokémon X and Y Retrospective: A Forgotten Chapter of the Franchise
I 100%'d Pokemon X & Y 10 Years Later, Here's What Happened
Комментарии
 0:02:20
0:02:20
 0:03:07
0:03:07
 0:03:43
0:03:43
 0:00:45
0:00:45
 0:02:42
0:02:42
 0:04:35
0:04:35
 0:02:19
0:02:19
 0:02:29
0:02:29
 0:03:17
0:03:17
 0:01:06
0:01:06
 0:50:43
0:50:43
 0:03:31
0:03:31
 0:04:07
0:04:07
 0:01:00
0:01:00
 0:03:03
0:03:03
 0:01:37
0:01:37
 0:04:40
0:04:40
 0:15:00
0:15:00
 0:01:45
0:01:45
 0:04:37
0:04:37
 0:17:14
0:17:14
 0:02:55
0:02:55
 0:40:53
0:40:53
 0:49:56
0:49:56