filmov
tv
Finding The Equation Of A Line Through 2 Points PART 2 | Graphs | Maths | FuseSchool

Показать описание
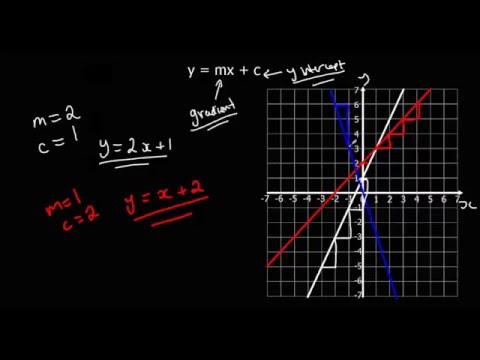
In this video we are going to look at how to find the equation of a straight line that passes through two given points (coordinates). You should already know that a straight line follows the y=mx+c format, where 'm' is the gradient and 'c' is the y-intercept. Start by finding the gradient either using gradient = rise / run or gradient = (y2 - y1) / (x2 - x1). This then gives you a value for the gradient 'm' so this can be substituted into the y=mx+c equation. Now the only unknown is the y-intercept 'c' so substitute in either sets of coordinates from the question in place of the 'x' and 'y' to find the unknown 'c'. You would then end up with the equation of the straight line that passes through the 2 points.
SUBSCRIBE to the FuseSchool YouTube channel for many more educational videos. Our teachers and animators come together to make fun & easy-to-understand videos in Chemistry, Biology, Physics, Maths & ICT.
These videos can be used in a flipped classroom model or as a revision aid.
Find all of our Chemistry videos here:
Find all of our Biology videos here:
Find all of our Maths videos here:
SUBSCRIBE to the FuseSchool YouTube channel for many more educational videos. Our teachers and animators come together to make fun & easy-to-understand videos in Chemistry, Biology, Physics, Maths & ICT.
These videos can be used in a flipped classroom model or as a revision aid.
Find all of our Chemistry videos here:
Find all of our Biology videos here:
Find all of our Maths videos here:
How To Find The Equation of a Line From a Graph | Algebra
How To Find The Equation of a Line Given Two Points
GCSE Maths - How to Find the Equation of a Straight Line (y = mx + c) #68
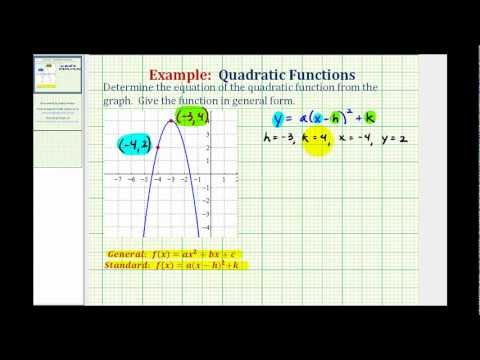
How To Find The Equation of a Quadratic Function From a Graph
Finding the equation of a straight line given the gradient and a point
NECO 2020 Question 30 | Equation of a straight line
GCSE Maths - Finding the Equation of a Straight Line From 2 Sets of Coordinates #69
Finding the equation of a line
Find the sum of all prime factors of 1998 #primefactorisation #fyp
Finding the Equation of a Line in Slope Y-Intercept Form
Finding the Equation of a Line Given Slope and a Point - Point - Slope Form
FINDING THE EQUATION OF A PARALLEL LINE
How to find the equation of a line given two points
Ex: Find the Equation of a Quadratic Function from a Graph
Pre Calculus: Finding the Equation of the Circle Given the Radius and Center
Find Equation of Line Perpendicular to a Line Through a Given Point
Finding the Equation of a Tangent
Find equation from the graph
Ex: Find the Equation of a Transformed Exponential Function From a Graph
Ex: Find the Equation of a Line in Slope Intercept Form Given the Slope and a Point
How To Find The Equation of a Plane Given a Point and Perpendicular Normal Vector
Writing the equation from a graph
How To Write The Equation of a Line Given The Slope and a Point | Algebra
Perpendicular Bisector Finding the Equation
Комментарии
 0:10:05
0:10:05
 0:07:38
0:07:38
 0:04:28
0:04:28
 0:09:35
0:09:35
 0:01:54
0:01:54
 0:05:52
0:05:52
 0:06:07
0:06:07
 0:09:04
0:09:04
 0:00:53
0:00:53
 0:04:28
0:04:28
 0:08:28
0:08:28
 0:01:57
0:01:57
 0:04:41
0:04:41
 0:04:56
0:04:56
 0:04:48
0:04:48
 0:02:26
0:02:26
 0:04:39
0:04:39
 0:05:29
0:05:29
 0:04:24
0:04:24
 0:03:37
0:03:37
 0:07:37
0:07:37
 0:02:09
0:02:09
 0:08:32
0:08:32
 0:02:51
0:02:51