filmov
tv
Evaluating a limit from a recursive sequence

Показать описание
How do we find the limit of a sequence if we are given the recursive formula? Note: this method might not always work. We have to know if the sequence converges or not first. This question can be for precalculus or calculus 2.
---------------------------------------------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie (10% off with the code "WELCOME10"):
---------------------------------------------------------
Best wishes to you,
#justcalculus
---------------------------------------------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie (10% off with the code "WELCOME10"):
---------------------------------------------------------
Best wishes to you,
#justcalculus
Evaluating Limits By Factoring
Calculus 1 - Introduction to Limits
How To Evaluate Limits From a Graph
Evaluate Limits | Calculus using calculator techniques
Infinite Limit Shortcut!! (Calculus)
Evaluating a limit by factoring
Limits and Continuity
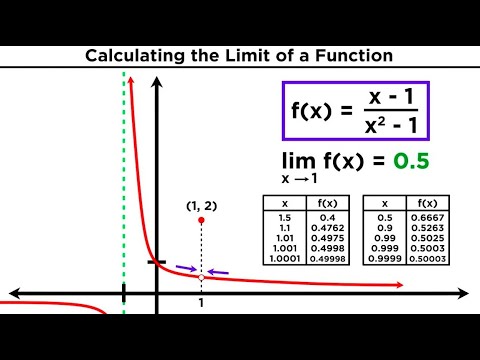
How to Find Any Limit (NancyPi)
AP Calculus AB (Evaluating Limit Using Riemann Sum Approximation Formula)
How To Find The Limit At Infinity
evaluating a limit using continuity
Limits and Limit Laws in Calculus
Learn how to evaluate a limit at infinity
Properties of Limits
Limits of Trigonometric Functions
Evaluating Limits from a Graph
Use Continuity to Evaluate a Limit
Limit Laws to Evaluate a Limit , Example 1
Evaluate Limit by using Algebraic techniques | Calculus Mathematics
This is a very famous limit
Evaluating A Limit | Calculus
Evaluating A Limit with Tangent and Sine
How To Find The Limit of a Polynomial Function - Calculus
How To Tell If The Limit Exists
Комментарии
 0:11:35
0:11:35
 0:20:20
0:20:20
 0:11:32
0:11:32
 0:00:57
0:00:57
 0:00:51
0:00:51
 0:04:46
0:04:46
 0:19:19
0:19:19
 0:16:42
0:16:42
 0:05:22
0:05:22
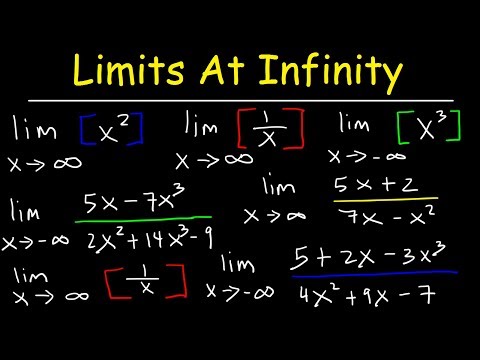 0:13:14
0:13:14
 0:02:16
0:02:16
 0:12:49
0:12:49
 0:01:40
0:01:40
 0:05:13
0:05:13
 0:15:23
0:15:23
 0:00:46
0:00:46
 0:01:32
0:01:32
 0:03:01
0:03:01
 0:00:33
0:00:33
 0:00:48
0:00:48
 0:00:32
0:00:32
 0:00:33
0:00:33
 0:03:49
0:03:49
 0:09:22
0:09:22