filmov
tv
Solving a System of Linear Equations with a Matrix and Python

Показать описание
Here's how to solve a system of linear equations.
Google CoLab Python
Install Jupyter Notebooks
Google CoLab Python
Install Jupyter Notebooks
How do we solve a system of linear equations using any method
Elimination Method For Solving Systems of Linear Equations Using Addition and Multiplication, Algebr
Solving Systems of Linear Equations By Graphing │Algebra
Solving Systems of Equations By Elimination & Substitution With 2 Variables
Solving Systems of Equations By Graphing
Solving linear systems by substitution | Algebra Basics | Khan Academy
Linear Algebra - Solving Systems of Equations
Solving System of Linear Equations by Substitution Method | Solution of System of Equations
How to use Canon F-789SGA Scientific Calculator to Solve Simultaneous Equations
Solving Linear Systems
Solving Systems of Equations With 3 Variables & Word Problems
Solving System of Linear Equations by Graphing - Math Teacher Gon
Solving linear systems by graphing | Systems of equations | 8th grade | Khan Academy
Substitution Method - Solving Systems of Linear Equations by │Algebra
Solving Systems of Equations... Elimination Method (NancyPi)
Solving a linear system of two equations by graphing
Solving System of Linear Equations by Elimination/ Addition Method
Solving systems of equations by elimination | Algebra Basics | Khan Academy
Solving a System of Linear Equations by Graphing - [8-5-21]
Solving System of Linear Equations: Matrix Inversion
Solving Systems of Linear and Quadratic Equations
Solving Systems of Linear Equations by Graphing
Solving a System of Linear Equations Using Inverses
Solving Linear Systems Using Matrices
Комментарии
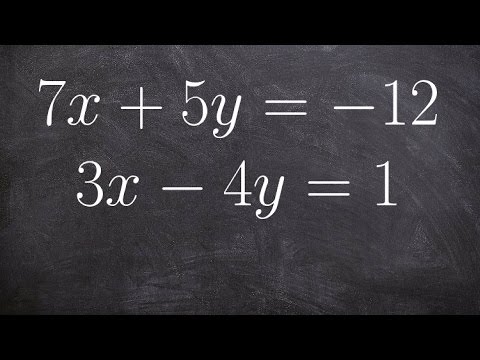 0:04:34
0:04:34
 0:10:21
0:10:21
 0:10:52
0:10:52
 0:10:27
0:10:27
 0:05:15
0:05:15
 0:09:21
0:09:21
 0:05:59
0:05:59
 0:12:28
0:12:28
 0:02:40
0:02:40
 0:15:48
0:15:48
 0:12:44
0:12:44
 0:10:47
0:10:47
 0:08:30
0:08:30
 0:12:16
0:12:16
 0:19:44
0:19:44
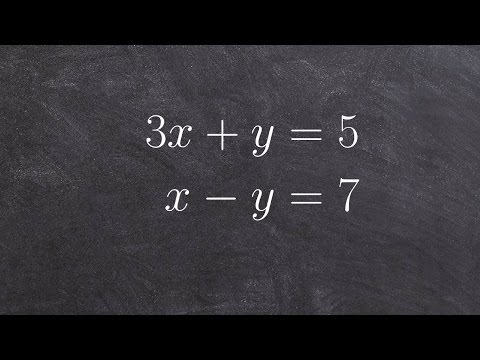 0:05:22
0:05:22
 0:09:55
0:09:55
 0:12:44
0:12:44
 0:18:47
0:18:47
 0:13:37
0:13:37
 0:13:36
0:13:36
 0:02:55
0:02:55
 0:06:28
0:06:28
 0:16:25
0:16:25